Argthtjtr

Cercle trigonométrique et angles remarquables

Planche sur la Trigonométrie, 1728 Cyclopaedia.

La trigonométrie (du grec τρίγωνος / trígonos, « triangulaire », et μέτρον / métron, « mesure ») est une branche des mathématiques qui traite des relations entre distances et angles dans les triangles et des fonctions trigonométriques telles que sinus, cosinus et tangente.

Présentation |

Histoire de la trigonométrie |

Premières techniques de mesure du triangle |

Cette section ne cite pas suffisamment ses sources (janvier 2011).  Pour l'améliorer, ajoutez des références vérifiables [comment faire ?] ou le modèle {{Référence nécessaire}} sur les passages nécessitant une source.

Les origines de la trigonométrie remontent aux civilisations d’Égypte antique, de Mésopotamie et de la vallée de l’Indus, il y a plus de 4 000 ans^[1]. Il semblerait que les Babyloniens aient basé la trigonométrie sur un système numérique à base 60.
Lagadha (ca -1350 ; ca -1200) aurait été le premier mathématicien à utiliser la géométrie et la trigonométrie pour l’astronomie et dont on retrouve une trace écrite ; la plupart de ses travaux auraient aujourd’hui disparu,^{[réf. nécessaire]}, mais son Vedanga Jyotisha nous est parvenu.

La tablette paléo-babylonienne Plimpton 322 (ca -1800) présenterait des rudiments de trigonométrie^[2].

La première utilisation du sinus apparaît dans les Śulba-Sūtras en Inde, entre ca -800 et ca -500^{[réf. nécessaire]}, où le sinus de ^π⁄₄ (ou 45°) est correctement calculé comme ¹⁄_√2 dans un problème de construction d’un cercle de même aire qu’un carré donné (le contraire de la quadrature du cercle).

Les astronomes grecs |

L'astronome et mathématicien grec Hipparque de Nicée (-190 ; -120) construisit les premières tables trigonométriques sous la forme de tables de cordes : elles faisaient correspondre à chaque valeur de l'angle au centre (avec une division du cercle en 360°), la longueur de la corde interceptée dans le cercle, pour un rayon fixe donné. Ce calcul correspond au double du sinus de l'angle moitié, et donne donc, d'une certaine façon, ce que nous appelons aujourd'hui une table de sinus. Toutefois, les tables d'Hipparque n'étant pas parvenues jusqu'à nous, elles ne nous sont connues que par le grec Ptolémée, qui les publia, vers l'an 150, avec leur mode de construction dans son Almageste. C'est ainsi qu'elles furent redécouvertes à la fin du Moyen Âge par Georg von Purbach et son élève Regiomontanus. On attribue à Ménélaos d'Alexandrie (fin du I^er siècle) des développements en trigonométrie sphérique, au moins partiellement présents dans l'Almageste et longtemps attribués à Ptolémée lui-même.

Le mathématicien indien Âryabhata, en 499, donne une table des sinus et des cosinus. Il utilise zya pour sinus, kotizya pour cosinus et otkram zya pour l'inverse du sinus. Il introduit aussi le sinus verse.

Un autre mathématicien indien, Brahmagupta, utilise en 628 l'interpolation numérique pour calculer la valeur des sinus jusqu'au second ordre.

Essor dans le monde musulman |

C'est dans le monde musulman que la trigonométrie prend le statut de discipline à part entière et se détache de l'astronomie^[3].

Omar Khayyam (1048-1131) combine l'utilisation de la trigonométrie et la théorie de l'approximation pour fournir des méthodes de résolutions d'équations algébriques par la géométrie. Des méthodes détaillées de constructions de tables de sinus et cosinus pour tous les angles sont écrites par le mathématicien Bhāskara II en 1150. Il développe aussi la trigonométrie sphérique. Au XIII^e siècle, Nasir al-Din Tusi, à la suite de Bhāskara, est probablement un des premiers à considérer la trigonométrie comme une discipline distincte des mathématiques. Enfin, au XIV^e siècle, Al-Kachi réalise des tables de fonctions trigonométriques lors de ses études en astronomie.

En Europe : redécouverte de Ptolémée |

En Europe, la trigonométrie se développe vers le milieu du XIV^e siècle avec la traduction en latin des œuvres de Ptolémée. Les pionniers en ce domaine sont Georg von Purbach et surtout son étudiant Regiomontanus. Suivent au début du XVI^e siècle les traités d'Oronce Finé, Pedro Nunes et Joachim Rheticus. Le mathématicien silésien Bartholomäus Pitiscus publie un travail remarquable sur la trigonométrie en 1595, dont le titre (Trigonometria) a donné son nom à la discipline. C'est le mathématicien flamand Adrien Romain qui introduit la notation moderne sin⁡α{displaystyle sin alpha }.

Applications |

Les applications de la trigonométrie sont extrêmement nombreuses. En particulier, elle est utilisée en astronomie et en navigation avec notamment la technique de triangulation. Les autres champs où la trigonométrie intervient sont (liste non exhaustive) : physique, électricité, électronique, mécanique, acoustique, optique, statistiques, économie, biologie, chimie, médecine, météorologie, géodésie, géographie, cartographie, cryptographie, informatique etc.

Trigonométrie |

Triangle ABC

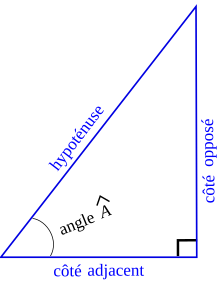
Une définition possible des fonctions trigonométriques est d'utiliser les triangles rectangles, c’est-à-dire les triangles qui possèdent un angle droit (90° degrés ou π/2 radians).

Et parce que la somme des angles d'un triangle fait 180° (ou π radians), l'angle le plus grand dans un tel triangle est l'angle droit. Le côté le plus long dans un triangle rectangle, c’est-à-dire le côté opposé à l'angle le plus grand (l'angle droit), s'appelle l'hypoténuse.

Dans la figure à droite, l'angle ACB^{displaystyle scriptstyle {widehat {ACB}}} forme l'angle droit. Le côté [AB] l'hypoténuse.

Les fonctions trigonométriques se définissent ainsi, en notant A l'angle BAC^{displaystyle scriptstyle {widehat {BAC}}} :

sin⁡A=côté opposéhypoténuse=accos⁡A=côté adjacenthypoténuse=bctan⁡A=côté opposécôté adjacent=ab{displaystyle sin A={{mbox{côté opposé}} over {mbox{hypoténuse}}}={a over c}qquad cos A={{mbox{côté adjacent}} over {mbox{hypoténuse}}}={b over c}qquad tan A={{mbox{côté opposé}} over {mbox{côté adjacent}}}={a over b}}

Ce sont les fonctions trigonométriques les plus importantes. Elles ont été définies pour les angles entre 0° et 90° (soit entre 0 et π/2 radians). En utilisant le cercle unité, on peut étendre cette définition.

Formules de trigonométrie |

Identité remarquable |

Quel que soit l'angle A, on a (d'après le théorème de Pythagore):

cos2⁡A+sin2⁡A=1{displaystyle cos ^{2}A+sin ^{2}A=1,}

Formules d'addition et de différence des arcs |

Les deux formules principales sont les formules d'addition pour le cosinus et le sinus :

cos⁡(A+B)=cos⁡Acos⁡B−sin⁡Asin⁡B{displaystyle cos(A+B)=cos Acos B-sin Asin B} ;

sin⁡(A+B)=sin⁡Acos⁡B+cos⁡Asin⁡B{displaystyle sin(A+B)=sin Acos B+cos Asin B}.

On en déduit celle pour la tangente :

tan⁡(A+B)=tan⁡A+tan⁡B1−tan⁡Atan⁡B{displaystyle tan(A+B)={frac {tan A+tan B}{1-tan Atan B}}},

ainsi que les formules de différence (en remplaçant B{displaystyle B} par −B{displaystyle -B}, sachant que la fonction cosinus est paire et les fonctions sinus et tangente sont impaires).

Formules de multiplication des arcs |

cos⁡(2a)=cos2⁡a−sin2⁡a=2cos2⁡a−1=1−2sin2⁡a{displaystyle cos(2a)=cos ^{2}a-sin ^{2}a=2cos ^{2}a-1=1-2sin ^{2}a,}

sin⁡(2a)=2sin⁡acos⁡a{displaystyle sin(2a)=2sin acos a,}

tan⁡(2a)=2tan⁡a1−tan2⁡a{displaystyle tan(2a)={frac {2tan a}{1-tan ^{2}a}},}

sin⁡(3a)=3sin⁡a−4sin3⁡a{displaystyle sin(3a)=3sin a-4sin ^{3}a,}

cos⁡(3a)=−3cos⁡a+4cos3⁡a{displaystyle cos(3a)=-3cos a+4cos ^{3}a,}

tan⁡(3a)=3tan⁡a−tan3⁡a1−3tan2⁡a{displaystyle tan(3a)={frac {3tan a-tan ^{3}a}{1-3tan ^{2}a}}}

Formules de développement et de factorisation (formules de Simpson) |

Des formules d'addition et de différence (voir supra), on déduit :

Développement

cos⁡Acos⁡B=cos⁡(A−B)+cos⁡(A+B)2{displaystyle cos Acos B={frac {cos(A-B)+cos(A+B)}{2}}}, en particulier cos2⁡A=1+cos⁡(2A)2{displaystyle cos ^{2}A={frac {1+cos(2A)}{2}}},

sin⁡Asin⁡B=cos⁡(A−B)−cos⁡(A+B)2{displaystyle sin Asin B={frac {cos(A-B)-cos(A+B)}{2}}}, en particulier sin2⁡A=1−cos⁡(2A)2{displaystyle sin ^{2}A={frac {1-cos(2A)}{2}}},

sin⁡Acos⁡B=sin⁡(A+B)+sin⁡(A−B)2{displaystyle sin Acos B={frac {sin(A+B)+sin(A-B)}{2}}} ;

Factorisation

cos⁡p+cos⁡q=2cos⁡p+q2cos⁡p−q2{displaystyle cos p+cos q=2cos {{p+q} over 2}cos {{p-q} over 2}},

cos⁡p−cos⁡q=−2sin⁡p+q2sin⁡p−q2{displaystyle cos p-cos q=-2sin {{p+q} over 2}sin {{p-q} over 2}},

sin⁡p+sin⁡q=2sin⁡p+q2cos⁡p−q2{displaystyle sin p+sin q=2sin {{p+q} over 2}cos {{p-q} over 2}}.

Formules de l'arc moitié |

Ces formules interviennent dans de très nombreux problèmes. En posant :

t=tan⁡A2{displaystyle t=tan {frac {A}{2}}},

on a :

sin⁡A=2t1+t2 ,cos⁡A=1−t21+t2 ,tan⁡A=2t1−t2{displaystyle sin A={frac {2t}{1+t^{2}}}~,qquad cos A={frac {1-t^{2}}{1+t^{2}}}~,qquad tan A={frac {2t}{1-t^{2}}}}.

Théorème d'Al-Kashi ou loi des cosinus |

a2=b2+c2−2bc⋅cos⁡A^{displaystyle a^{2}=b^{2}+c^{2}-2,b,c,cdot cos {widehat {A}}}.

Cette formule a une importance particulière en triangulation et a servi à l'origine en astronomie. On doit au mathématicien Ghiyath al-Kashi, de l'école de Samarcande, de mettre le théorème sous une forme utilisable pour la triangulation au cours du XV^e siècle.

Remarque : lorsque A^=90∘{displaystyle {hat {A}}=90^{circ }} ou π/2{displaystyle pi /2}, on a a2=b2+c2{displaystyle a^{2}=b^{2}+c^{2}}, c'est-à-dire le théorème de Pythagore.

Résoudre un triangle |

C’est, étant donné un côté et deux angles adjacents, ou un angle et deux côtés adjacents, ou à la rigueur deux côtés b et c et leur angle B, trouver le triangle correspondant, c’est-à-dire a, b, c, A, B et C (et vérifier une des règles non appliquée dans le processus).

On résout ce genre de problème à l’aide des formules précédentes (plus la formule de projection évidente a = b · cos C + c · cos B).

Par exemple :

Sur l’axe Ox, OB = 1 et OC = 1,5. OBM = 60° et OCM = 30°. Trouver M :

Faire l’épure ; M se trouve en (x = 0,75 ; y = 0,45) environ.

Raisonner : dans le triangle BMC, B = 120° et C = 30° donc M = 30° ; donc le triangle est isocèle en B et BM'= 0,5.

Puis CM=2×0,5×cos⁡(C)=32{displaystyle CM=2times 0,5times cos(C)={{sqrt {3}} over 2}}.

Soit H la projection de M sur l’axe : HM = y et l'angle HMB vaut 30°.

y=34≈0,43{displaystyle y={{sqrt {3}} over 4}approx 0,43} et x=1−14=34=0,75{displaystyle x=1-{1 over 4}={3 over 4}=0,75}.

La distance OM=32=MC{displaystyle OM={{sqrt {3}} over 2}=MC}, l’azimut de M vaut 30°, et l’angle OMB vaut 90°.

Il est rare que ce soit aussi simple en pratique.

En général, on demande quatre à six chiffres significatifs. Les calculettes ont considérablement réduit le travail assez fastidieux de « réduction des triangles ».
Rappelons que la mesure du degré de l’arc méridien terrestre de Paris s’est effectuée de la sorte entre Malvoisine et Montlhéry par l’abbé Picard, dans le milieu du XVII^e siècle.

Aire du triangle |

L'aire A du triangle se détermine à l'aide de la longueur de deux côtés et du sinus de l'angle qu'ils forment :

A=12a×b×sin⁡(C^){displaystyle A={frac {1}{2}}atimes btimes sin({hat {C}})}.

D'une telle égalité, appliquée à chaque sommet du triangle, on peut déduire la loi des sinus.

La formule précédente, complétée par la loi des cosinus, permet également d'établir la formule de Héron :

A=p(p−a)(p−b)(p−c){displaystyle A={sqrt {p(p-a)(p-b)(p-c)}}},

où a, b et c sont les longueurs de ses côtés et p désigne le demi-périmètre du triangle :

p=(a+b+c)2{displaystyle p={(a+b+c) over 2}}.

Quelques problèmes célèbres |

• La flèche d’une corde AB sous-tendant l’arc AOB = 2 α : soit I le milieu de AB, et CD le diamètre passant par I ; alors :
  

  ID=→f⋅(2R−f)=(R⋅sin⁡(α))2{displaystyle ID=rightarrow fcdot (2R-f)=(Rcdot sin(alpha ))^{2}}

  
  


• Aire de l'onglet :
  

  
  

  
  S=R2⋅[α−sin⁡(2α)2]{displaystyle S=R^{2}cdot [alpha -{{sin(2alpha )} over 2}]} ;

  
  

  Quand α est petit, on compare cette aire à celle de la parabole osculatrice 13⋅f⋅AB{displaystyle {1 over 3}cdot fcdot AB} (théorème d'Archimède) : la différence est d'ordre supérieur à trois.

  
  

  
  


• 
  John Machin a été le premier à calculer π avec 100 décimales, en 1706, grâce à sa formule. Des formules de ce type ont été utilisées jusqu’à nos jours, pour calculer un grand nombre de décimales de π.


• Polygones réguliers constructibles à la règle et au compas :
  

  
  

  l’heptagone et l’ennéagone ne sont pas constructibles, mais le polygone à 17 côtés (heptadécagone) est constructible (théorème de Gauss-Wantzel).

  
  

  En revanche, on peut construire par pliage l’heptagone et l’ennéagone.

  
  

  On prouve également que pour A=2π7{displaystyle A={{2pi } over 7}} (intervenant dans la construction de l’heptagone par pliage), on a :
  

  
  

  
  sin⁡(A)⋅sin⁡(2A)⋅sin⁡(3A)=78{displaystyle sin(A)cdot sin(2A)cdot sin(3A)={{sqrt {7}} over 8}} et

  
  

  
  cos⁡(A)⋅cos⁡(2A)⋅cos⁡(3A)=18{displaystyle cos(A)cdot cos(2A)cdot cos(3A)={1 over 8}}.

  
  

  
  

  
  

  Des formules semblables existent pour l'ennéagone.

  
  

  
  

Notes et références |

Voir aussi |

Articles connexes |

• Cercle unité


• Cercle trigonométrique


• Fonction hyperbolique


• Sens trigonométrique


• Trigonométrie complexe


• Trigonométrie de Wildberger


• CORDIC

• Portail des mathématiques