Argthtjtr

Pour les articles homonymes, voir Surface.

Ne pas confondre avec les notions de superficie ou d'aire comme mesure d'un espace concret avec une unité de mesure; voir Surface, aire et superficie.

En géométrie analytique, on représente les surfaces, c'est-à-dire les ensembles de points sur lequel il est localement possible de se repérer à l'aide de deux coordonnées réelles, par des relations entre les coordonnées de leurs points, qu'on appelle équations de la surface
ou par des représentations paramétriques.

Cet article étudie les propriétés des surfaces que cette approche (appelée souvent extrinsèque) permet de décrire. Pour des résultats plus approfondis, voir Géométrie différentielle des surfaces.

Propriétés affines |

On suppose dans tout cet article qu'on a muni l'espace d'un repère, dans lequel sont exprimées toutes les coordonnées.

Représentation paramétrique |

Une nappe paramétrée est la donnée de trois fonctions de deux variables (définies sur un disque ouvert, un rectangle ou
plus généralement un ouvert de R2{displaystyle mathbb {R} ^{2}})

x=f(u,v),y=g(u,v)z=h(u,v){displaystyle x=f(u,v),,y=g(u,v),z=h(u,v)}.

qui représentent les coordonnées d'un point M par rapport à un repère (O,i→,j→,k→){displaystyle (O,{overrightarrow {i}},{overrightarrow {j}},{overrightarrow {k}})}

On a envie de dire qu'une surface est l'image d'une nappe paramétrée. Mais quelques précautions sont nécessaires : si on prend f(u,v)=u, g(u,v)=h(u,v)=0 on a une nappe paramétrée dont l'image est une droite.

Dans le cas où F→=(f,g,h){displaystyle {overrightarrow {F}}=(f,g,h)} est injective, tout point M de S admet un couple unique (u,v) pour antécédent.

Un cas particulier important de nappe paramétrée est celui du graphe d'une fonction de deux variables :
lorsque x=u,y=v,z=h(u,v){displaystyle x=u,y=v,z=h(u,v)}. On obtient alors une surface représentée par l’équation cartésienne z=h(x,y){displaystyle z=h(x,y)}.

Équation d'une surface |

Étant donnée une fonction H de trois variables, l'ensemble des points M dont les coordonnées, dans le repère que l'on s'est donné
vérifientH(x,y,z)=0 est une surface.
Lorsqu'au voisinage d'un point (x0,y0,z0){displaystyle (x_{0},y_{0},z_{0})} de S, l'équation H(x,y,z)=0{displaystyle H(x,y,z)=0} peut être résolue en z, on est ramené, dans ce voisinage, à l'équation cartésienne z=h(x,y){displaystyle z=h(x,y)}. C'est le cas quand ∂H∂z(x0,y0,z0)≠0{displaystyle {frac {partial H}{partial z}}(x_{0},y_{0},z_{0})not =0}.

Plus de précisions |

Si on se contente des points de vue qui précèdent, on obtient des exemples qu'il vaudrait mieux exclure (cf. la nappe (u,v)↦(u,0,0){displaystyle (u,v)mapsto (u,0,0)}). De plus passer du paramétrage à une équation ou inversement n'a rien d'évident.

Une nappe paramétrée F→=(f,g,h){displaystyle {overrightarrow {F}}=(f,g,h)} est régulière si

1. 
   F→{displaystyle {overrightarrow {F}}} est de classe C1{displaystyle C^{1}}
   


2. les vecteurs ∂F→∂u{displaystyle {frac {partial {overrightarrow {F}}}{partial u}}} et ∂F→∂v{displaystyle {frac {partial {overrightarrow {F}}}{partial v}}} sont partout linéairement indépendants.

Exemples

• La nappe paramétrée associée à une surface d'équation cartésienne z=h(x,y) est régulière (si h est C1{displaystyle C^{1}})

• Si F est C1{displaystyle C^{1}}, et si ses dérivées partielles ne s'annulent pas simultanément sur F−1(0){displaystyle F^{-1}(0)}, alors F−1(0){displaystyle F^{-1}(0)} est localement un graphe, d'après le théorème des fonctions implicites.

En fait, un cas particulier du théorème des fonctions implicites est le résultat suivant.

En pratique, les surfaces que l'on étudie sont le plus souvent des réunions d'image de nappes régulières. Quand ce n'est pas le cas, on regarde au cas par cas.

Exemples |

• La sphère de centre O et de rayon 1 a pour équation x2+y2+z2=1{displaystyle x^{2}+y^{2}+z^{2}=1}. On peut aussi considérer la nappe paramétrée

(u,v)↦(cos⁡ucos⁡v,sin⁡ucos⁡v,sin⁡v){displaystyle (u,v)mapsto (cos ucos v,sin ucos v,sin v)}

qui est régulière et injective sur [0,2π[×]−π2,π2[{displaystyle [0,2pi [times ]-{frac {pi }{2}},{frac {pi }{2}}[} mais non surjective. Les nombres u et v correspondent à la longitude et à la latitude des géographes. Mais la régularité se perd pour v=±π2{displaystyle v=pm {frac {pi }{2}}}. En tout état de cause, il est impossible de réaliser la sphère tout entière avec une nappe régulière injective : une telle nappe donnerait un homéomorphisme de la sphère avec un ouvert du plan.

• l'équation z2=x2+y2{displaystyle z^{2}=x^{2}+y^{2}} représente le cône de révolution d'axe Oz et d'angle π4{displaystyle {frac {pi }{4}}}.

C'est l'image de la nappe paramétrée

(r,θ)↦(rcos⁡θ,rsin⁡θ,r){displaystyle (r,theta )mapsto (rcos theta ,rsin theta ,r)}

qui est régulière si r≠0{displaystyle rnot =0}.

• une surface de révolution d'axe Oz peut être réalisée par une équation de la forme F(r,z)=0{displaystyle F(r,z)=0} (avec r=x2+y2{displaystyle r={sqrt {x^{2}+y^{2}}}}) ou une nappe paramétrée (r,θ)↦(rcos⁡θ,rsin⁡θ,f(r)){displaystyle (r,theta )mapsto left(rcos theta ,rsin theta ,f(r)right)}.

Courbes coordonnées |

Représentation des courbes coordonnées d'une surface S.

Soit S la surface définie par OM→=F→(u,v){displaystyle {overrightarrow {OM}}={overrightarrow {F}}(u,v)} avec v=v0{displaystyle v=v_{0}} (constante), cette surface d'équation OM→=F→(u,v0){displaystyle {overrightarrow {OM}}={overrightarrow {F}}(u,v_{0})} est appelée courbe coordonnée Cv0{displaystyle C_{v_{0}}}.

Quand v0{displaystyle v_{0}} parcourt toutes les valeurs acceptables v0,v1,v2,...vn{displaystyle v_{0},v_{1},v_{2},...v_{n}}, la réunion des courbes Cv0,Cv1,Cv2,...Cvn,{displaystyle C_{v_{0}},C_{v_{1}},C_{v_{2}},...C_{v_{n}},} est la surface S.

Le même procédé vaut pour la définition des courbes Cu0{displaystyle C_{u_{0}}} d'équation OM→=F→(u0,v){displaystyle {overrightarrow {OM}}={overrightarrow {F}}(u_{0},v)}.

Courbe tracée sur une surface |

Elle est définie par une application t↦f(u,v){displaystyle tmapsto f(u,v)} et est constituée de l'ensemble des points M d'équation :

OM→=F→(u(t),v(t)){displaystyle {overrightarrow {OM}}={overrightarrow {F}}(u(t),v(t))}, contenue dans S et dite tracée sur S.

Tangentes et plan tangent à une surface |

On appelle tangente à une surface S au point M0{displaystyle M_{0}} toute tangente à une courbe tracée sur S contenant M0{displaystyle M_{0}}.

Soit f{displaystyle f} une fonction (u,v)↦OM→(u,v){displaystyle (u,v)mapsto {overrightarrow {OM}}(u,v)} et, au voisinage de u0,v0{displaystyle u_{0},v_{0}}, les dérivées partielles vectorielles ∂M→∂u{displaystyle {frac {overrightarrow {partial M}}{partial u}}} et ∂M→∂v{displaystyle {frac {overrightarrow {partial M}}{partial v}}} continues en u0,v0{displaystyle u_{0},v_{0}}.

Si les vecteurs ∂M→∂u{displaystyle {frac {overrightarrow {partial M}}{partial u}}} et ∂M→∂v{displaystyle {frac {overrightarrow {partial M}}{partial v}}} sont indépendants (non colinéaires), tous les vecteurs tangents en M0{displaystyle M_{0}} aux courbes tracées sur S{displaystyle S} et passant par ce point
sont dans le plan passant par M0{displaystyle M_{0}} et contenant ces deux vecteurs.
C'est par définition le plan tangent à S{displaystyle S} au point M0{displaystyle M_{0}}.

Soit un plan tangent défini par le point M0(x0,y0,z0){displaystyle M_{0}(x_{0},y_{0},z_{0})}, et deux vecteurs non colinéaires :

∂M→∂u0=(∂x∂u0,∂y∂u0,∂z∂u0){displaystyle {frac {overrightarrow {partial M}}{partial u_{0}}}=left({frac {partial x}{partial u_{0}}},{frac {partial y}{partial u_{0}}},{frac {partial z}{partial u_{0}}}right)}, et

∂M→∂v0=(∂x∂v0,∂y∂v0,∂z∂v0){displaystyle {frac {overrightarrow {partial M}}{partial v_{0}}}=left({frac {partial x}{partial v_{0}}},{frac {partial y}{partial v_{0}}},{frac {partial z}{partial v_{0}}}right)}

Son équation est :

|x−x0∂x∂u0∂x∂v0y−y0∂y∂u0∂y∂v0z−z0∂z∂u0∂z∂v0|=0{displaystyle {begin{vmatrix}x-x_{0}&{frac {partial x}{partial u_{0}}}&{frac {partial x}{partial v_{0}}}\y-y_{0}&{frac {partial y}{partial u_{0}}}&{frac {partial y}{partial v_{0}}}\z-z_{0}&{frac {partial z}{partial u_{0}}}&{frac {partial z}{partial v_{0}}}end{vmatrix}}=0,}

Par exemple si l'équation de S{displaystyle S,} est de la forme z=h(x,y){displaystyle z=h(x,y),}, en posant
p=hx′(x0,y0),{displaystyle p=h_{x}^{prime }(x_{0},y_{0}),} et q=hy′(x0,y0),{displaystyle q=h_{y}^{prime }(x_{0},y_{0}),} on a :

z−z0=p(x−x0)+q(y−y0){displaystyle z-z_{0}=p(x-x_{0})+q(y-y_{0}),}

Si l'équation de S{displaystyle S,} est de forme implicite f(x,y,z)=0{displaystyle f(x,y,z)=0,} et si l'une des dérivées partielles de f en (x0,y0,z0){displaystyle (x_{0},y_{0},z_{0})} est non nulle, on peut se ramener au cas ci-dessus grâce au théorème des fonctions implicites.
Par exemple si fz′(x0,y0,z0)≠0{displaystyle f_{z}^{prime }(x_{0},y_{0},z_{0})not =0}, on peut écrire z=h(x,y){displaystyle z=h(x,y),}, et l'on a

hx′(x0,y0)=−fx′(x0,y0,z0)fz′(x0,y0,z0) et hy′(x0,y0)=−fy′(x0,y0,z0)fz′(x0,y0,z0){displaystyle h_{x}^{prime }(x_{0},y_{0})=-{frac {f'_{x}(x_{0},y_{0},z_{0})}{f'_{z}(x_{0},y_{0},z_{0})}} mathrm {et} h_{y}^{prime }(x_{0},y_{0})=-{frac {f'_{y}(x_{0},y_{0},z_{0})}{f'_{z}(x_{0},y_{0},z_{0})}},}

L'équation du plan tangent s'écrit alors

(x−x0)fx′(x0,y0,z0)+(y−y0)fy′(x0,y0,z0)+(z−z0)fz′(x0,y0,z0)=0{displaystyle (x-x_{0})f'_{x}(x_{0},y_{0},z_{0})+(y-y_{0})f'_{y}(x_{0},y_{0},z_{0})+(z-z_{0})f'_{z}(x_{0},y_{0},z_{0})=0}

ou, sous forme vectorielle,

M0M→⋅grad f(M0)=0{displaystyle {overrightarrow {M_{0}M}}cdot mathbf {grad} ~f(M_{0})=0}

Propriétés métriques |

Normale à une surface |

Le plan tangent à la surface S{displaystyle S,} au point M0{displaystyle M_{0},} est engendré par les vecteurs ∂M→∂u0{displaystyle {frac {overrightarrow {partial M}}{partial u_{0}}}} et ∂M→∂v0{displaystyle {frac {overrightarrow {partial M}}{partial v_{0}}}}.

On appelle normale à la surface S{displaystyle S,} au point M0{displaystyle M_{0},} la normale au plan tangent : elle admet donc pour vecteur directeur ∂M→∂u0∧∂M→∂v0{displaystyle {frac {overrightarrow {partial M}}{partial u_{0}}}wedge {frac {overrightarrow {partial M}}{partial v_{0}}}}.

Ses équations sont :

x−x0∂(y,z)∂(u0,v0)=y−y0∂(z,x)∂(u0,v0)=z−z0∂(x,y)∂(u0,v0){displaystyle {frac {x-x_{0}}{frac {partial (y,z)}{partial (u_{0},v_{0})}}}={frac {y-y_{0}}{frac {partial (z,x)}{partial (u_{0},v_{0})}}}={frac {z-z_{0}}{frac {partial (x,y)}{partial (u_{0},v_{0})}}}}

avec, par exemple, le jacobien ∂(y,z)∂(u0,v0){displaystyle {frac {partial (y,z)}{partial (u_{0},v_{0})}}} égal à |∂y∂u0∂y∂v0∂z∂u0∂z∂v0|{displaystyle {begin{vmatrix}{frac {partial y}{partial u_{0}}}&{frac {partial y}{partial v_{0}}}\{frac {partial z}{partial u_{0}}}&{frac {partial z}{partial v_{0}}}end{vmatrix}}}.

Dans le cas où la surface S{displaystyle S,} est définie par une équation cartésienne z=h(x,y){displaystyle z=h(x,y)}, l'équation de la normale en S{displaystyle S,} au point M0{displaystyle M_{0},} est donnée par

x−x0p=y−y0q=z−z0−1{displaystyle {frac {x-x_{0}}{p}}={frac {y-y_{0}}{q}}={frac {z-z_{0}}{-1}},}

Dans le cas où la surface S{displaystyle S,} est définie par une équation implicite f(x,y,z){displaystyle f(x,y,z)}, la normale en S{displaystyle S,} au point M0{displaystyle M_{0},} a pour vecteur directeur le gradient de f{displaystyle f,} en M0{displaystyle M_{0},}, et l'équation s'écrit

(x−x0)fx′(x0,y0,z0)=(y−y0)fy′(x0,y0,z0)=(z−z0)fz′(x0,y0,z0){displaystyle {frac {(x-x_{0})}{f_{x}^{prime }(x_{0},y_{0},z_{0})}}={frac {(y-y_{0})}{f_{y}^{prime }(x_{0},y_{0},z_{0})}}={frac {(z-z_{0})}{f_{z}^{prime }(x_{0},y_{0},z_{0})}},}

ou, sous forme vectorielle :

M0M→=ρ⋅grad f(M0),ρ∈R{displaystyle {overrightarrow {M_{0}M}}=rho cdot mathbf {grad} ~f(M_{0}),rho in mathbb {R} }

Intersection de deux surfaces |

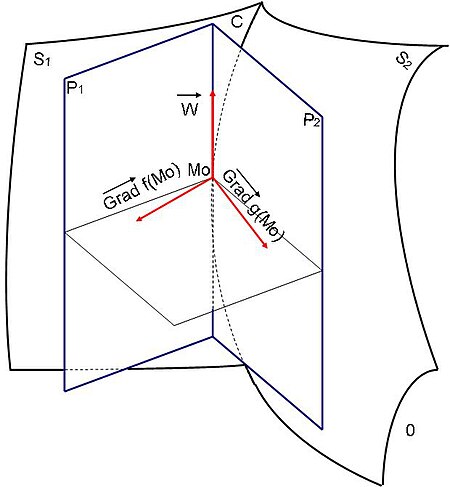
Soit la courbe C{displaystyle C,}, intersection des surfaces S1{displaystyle S_{1},} et S2{displaystyle S_{2},} dont les équations sont :

S1↦f(x,y,z)=0{displaystyle S_{1}mapsto f(x,y,z)=0}, et S2↦g(x,y,z)=0{displaystyle S_{2}mapsto g(x,y,z)=0}.

Ces deux surfaces admettent chacune un plan tangent en M0(x0,y0,z0){displaystyle M_{0}(x_{0},y_{0},z_{0})}, respectivement notés P1{displaystyle P_{1},} et P2{displaystyle P_{2},}.

La droite résultant de l'intersection des plans P1{displaystyle P_{1},} et P2{displaystyle P_{2},} est la tangente en M0{displaystyle M_{0}} à C{displaystyle C,}.

Elle admet pour vecteur directeur :

W→=grad f(M0)∧grad g(M0){displaystyle {overrightarrow {W}}=mathbf {grad} ~f(M_{0})wedge mathbf {grad} ~g(M_{0})}

Soit l'équation :

x−x0∂(f,g)∂(y0,z0)=y−y0∂(f,g)∂(z0,x0)=z−z0∂(f,g)∂(x0,y0){displaystyle {frac {x-x_{0}}{frac {partial (f,g)}{partial (y_{0},z_{0})}}}={frac {y-y_{0}}{frac {partial (f,g)}{partial (z_{0},x_{0})}}}={frac {z-z_{0}}{frac {partial (f,g)}{partial (x_{0},y_{0})}}}}

L'équation du plan normal à C{displaystyle C,} en M0{displaystyle M_{0},} est le plan défini par M0,grad f(M0),grad g(M0){displaystyle M_{0},mathbf {grad} ~f(M_{0}),mathbf {grad} ~g(M_{0}),},

Son équation est :

|x−x0∂f∂x(M0)∂g∂x(M0)y−y0∂f∂y(M0)∂g∂y(M0)z−z0∂f∂z(M0)∂g∂z(M0)|=0{displaystyle {begin{vmatrix}x-x_{0}&{frac {partial f}{partial x}}(M_{0})&{frac {partial g}{partial x}}(M_{0})\y-y_{0}&{frac {partial f}{partial y}}(M_{0})&{frac {partial g}{partial y}}(M_{0})\z-z_{0}&{frac {partial f}{partial z}}(M_{0})&{frac {partial g}{partial z}}(M_{0})end{vmatrix}}=0,}

Voir aussi |

Bibliographie |

• 
  Michèle Audin, Géométrie (chap. 8), Belin 2008, (ISBN 2-7011-2130-2)
  

Articles connexes |

• Surface de révolution


• Surface réglée


• Dérivation vectorielle


• Propriétés métriques des droites et plans


• Gradient


• Intégrale de surface


• Géométrie différentielle des surfaces

• Portail de la géométrie