Global Positioning System
Le Global Positioning System (GPS) (en français : « Système mondial de positionnement » [littéralement] ou « Géo-positionnement par satellite »), originellement connu sous le nom de Navstar GPS, est un système de positionnement par satellites appartenant au gouvernement des États-Unis. Mis en place par le département de la Défense des États-Unis à des fins militaires à partir de 1973, le système avec 24 satellites est totalement opérationnel en 1995 et s'ouvre au civil en 2000.
Les signaux transmis par les satellites peuvent être librement reçus et exploités par quiconque. L'utilisateur, qu'il soit sur terre, sur mer ou dans les airs, peut connaître sa position à toute heure et en tout lieu sur la surface ou au voisinage de la surface de la terre avec une précision sans précédent, dès lors qu'il est équipé d'un récepteur GPS et du logiciel nécessaire au traitement des informations reçues.
Le principe de fonctionnement repose sur la trilatération de signaux électromagnétiques synchronisés émis par les satellites. Pour assurer la précision du positionnement, le système GPS utilise des technologies sophistiquées : horloges atomiques embarquées, compensation d'effets relativistes, mise en place de stations d'observation et de synchronisation. Les coordonnées terrestres calculées se réfèrent au système géodésique WGS 84.
Commercialement, le GPS connait un grand succès et engendre de nombreux développements dans une multitude de domaines : navigations maritime, terrestre et aérienne, localisation de flottilles commerciales (bateaux, avions, camions), suivi et traçage de parcours, évaluation de la pertinence d'itinéraire. L'intégration de « puces GPS » dans les smartphones multiplie les usages domestiques ou individuels. Dans le milieu scientifique la précision de la localisation et de la synchronisation permettent de développer et d'exploiter de nouvelles applications : géodésie, synchronisation entre horloges atomiques, étude de l'atmosphère, etc.
L'Europe, la Chine, la Russie et l'Inde, conscients de l'intérêt stratégique d'un tel système de positionnement par satellites développent depuis quelques années des systèmes concurrents.

Un satellite NAVSTAR (Navigation Satellite Timing And Ranging) appartenant à la constellation du GPS.

Système de navigation GPS dans un taxi.

Radionavigation par GPS à bord d'un ULM.
Sommaire
1 Présentation
2 Histoire
3 Composition
3.1 Segment spatial
3.2 Segment de contrôle
3.3 Segment utilisateur
4 Principe de fonctionnement
4.1 Signal émis
4.2 Mesure de la distance du récepteur par rapport à un satellite
4.3 Calcul de la position
4.4 Résolution de l'équation de navigation
4.5 Décalage de l'horloge du récepteur
4.6 Erreurs possibles
4.7 Corrections troposphérique et ionosphérique
5 Amélioration locale du calcul
5.1 DGPS
5.2 SBAS
6 Conversion des informations obtenues
6.1 Positionnement
6.2 Temps et synchronisation
6.3 Visualisation cartographique
7 GPS et théorie de la relativité
8 Inconvénients du GPS
8.1 Dépendance stratégique
8.2 Limitations des récepteurs civils
8.3 Risque de surveillance abusive
8.4 Confiance exagérée dans ses performances
9 Autres systèmes de positionnement par satellites
10 Notes et références
10.1 Notes
10.2 Références
11 Voir aussi
11.1 Bibliographie
11.2 Articles connexes
11.3 Liens externes
Présentation |
Le GPS comprend au moins 24 satellites orbitant à 20 200 km d'altitude. Ces satellites émettent en permanence sur deux fréquences L1 (1 575,42 MHz) et L2 (1 227,60 MHz) modulées en phase (BPSK) par un ou plusieurs codes pseudo-aléatoires, datés précisément grâce à leur horloge atomique, et par un message de navigation. Ce message, transmis à 50 bit/s, inclut en particulier les éphémérides permettant le calcul de la position des satellites, ainsi que des informations sur leur horloge interne. Les codes sont un code C/A (acronyme de « coarse acquisition », en français : « acquisition brute ») de débit 1,023 Mbit/s et de période 1 ms, et un code P (pour « précis ») de débit 10,23 Mbit/s et de période 1 semaine. Le premier est librement accessible, le second est réservé aux utilisateurs autorisés car il est le plus souvent chiffré : on parle alors de code Y. Les récepteurs commercialisés dans le domaine civil utilisent le code C/A. Quelques récepteurs pour des applications de haute précision, comme la géodésie, mettent en œuvre des techniques permettant d'utiliser le code P malgré son chiffrage en code Y.
Ainsi, un récepteur GPS qui capte les signaux d'au moins quatre satellites équipés de plusieurs horloges atomiques peut, en calculant les temps de propagation de ces signaux entre les satellites et lui, connaître sa distance par rapport à ceux-ci et, par trilatération, situer précisément en trois dimensions n'importe quel point placé en visibilité des satellites GPS[1], avec une précision de 3 à 50 mètres pour le système standard. Le GPS est ainsi utilisé pour localiser des véhicules roulants, des navires, des avions, des missiles et même des satellites évoluant en orbite basse.
Concernant la précision, il est courant d'avoir une position horizontale à 10 mètres près.
Le GPS étant un système développé pour les militaires américains, une disponibilité sélective a été prévue : certaines informations, en particulier celles concernant l'horloge des satellites, peuvent être volontairement dégradées et priver les récepteurs qui ne disposent pas des codes correspondants de la précision maximale. Pendant quelques années, les civils n'avaient ainsi accès qu'à une faible précision (environ 100 m). Le 1er mai 2000, le président Bill Clinton a annoncé qu'il mettait fin à cette dégradation volontaire du service[2].
Certains systèmes GPS conçus pour des usages très particuliers peuvent fournir une localisation à quelques millimètres près. Le GPS différentiel (DGPS) corrige ainsi la position obtenue par GPS conventionnel par les données envoyées par une station terrestre de référence localisée très précisément. D'autres systèmes autonomes, affinant leur localisation au cours de huit heures d'exposition parviennent à des résultats équivalents.
Dans certains cas, seuls trois satellites peuvent suffire. La localisation en altitude (axe des Z) n'est pas d'emblée correcte alors que la longitude et la latitude (axe des X et des Y) sont encore bonnes. On peut donc se contenter de trois satellites lorsque l'on évolue au-dessus d'une surface « plane » (océan, mer). Ce type d'exception est surtout utile au positionnement d'engins volants (tels les avions) qui ne peuvent pas se reposer sur le seul GPS, trop imprécis pour leur donner leur altitude. Mais il existe néanmoins un modèle de géoïde mondial nommé « Earth Gravity Model 1996 » ou EGM96[3] associé au WGS 84 qui permet, à partir des coordonnées WGS 84, de déterminer[4] des altitudes rapportées au niveau moyen des mers avec une précision d'environ 1 mètre. Des récepteurs GPS évolués incluent ce modèle pour fournir des altitudes plus conformes à la réalité.
Histoire |
Cette section ne cite pas suffisamment ses sources (juillet 2017). Pour l'améliorer, ajoutez des références vérifiables [comment faire ?] ou le modèle {{Référence nécessaire}} sur les passages nécessitant une source. |
À l'origine, le GPS était un projet de recherche des Forces armées des États-Unis. Il a été lancé à la fin des années 1960 à la demande du président Richard Nixon. La réalisation a été confiée à Ivan A. Getting qui a conçu le principe d'un groupe de satellites gravitant en orbite et émettant des ondes radio UHF captées par des récepteurs GPS.
Il est basé sur des programmes précédents dont SECOR, une série de satellites utilisés pour effectuer des mesures géodésiques.
Le premier satellite est lancé en 1978. En 1995, le déploiement des 24 satellites opérationnels (plus 4 en réserve) est achevé. Le système devient alors fonctionnel[5].
En 1983, le président Ronald Reagan, à la suite de la mort des 269 passagers du vol 007 Korean Airlines, propose que la technologie GPS soit disponible gratuitement aux civils, une fois opérationnelle. Une seconde série de satellites est lancée à partir de 1989 en vue de constituer une flotte suffisante.
En 1995, le nombre de satellites disponibles permet de rendre le GPS opérationnel en permanence sur l'ensemble de la planète, avec une précision limitée à une centaine de mètres pour un usage civil. En 2000, le président Bill Clinton confirme l'intérêt de la technologie à des fins civiles et autorise une diffusion non restreinte des signaux GPS, permettant une précision d'une dizaine de mètres et une démocratisation de la technologie au grand public à partir du milieu des années 2000[6].
Les États-Unis continuent de développer leur système par le remplacement et l'ajout de satellites ainsi que par la mise à disposition de signaux GPS complémentaires, plus précis et demandant moins de puissance aux appareils de réception. Un accord d'interopérabilité a également été confirmé entre les systèmes GPS et Galileo afin que les deux systèmes puissent utiliser les mêmes fréquences et assurer une compatibilité entre eux.
Deux autres systèmes ont été mis au point par la Russie, le GLONASS à partir de 1980, et par la Chine, le Beidou initié en 2000.
Composition |
Le GPS se compose de trois groupes d'éléments (appelés segments) : des satellites en orbite autour de la Terre (segment spatial) ; des stations de contrôle au sol (segment contrôle) ; et les récepteurs GPS des utilisateurs (segment utilisateur)[7].
Segment spatial |
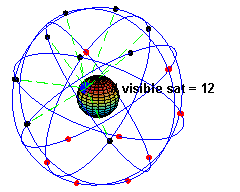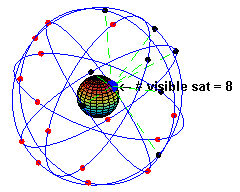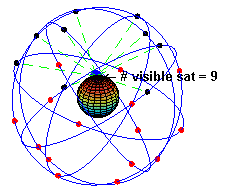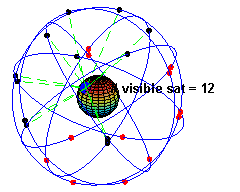
La constellation des satellites du GPS
Le segment spatial est constitué d'une constellation de 31 satellites en fonctionnement[7], mais le nombre de satellites en service à une date précise peut varier (cf. tableau) selon les opérations décidées par le segment de contrôle. La constellation est organisée autour de 24 satellites principaux qui assurent la disponibilité mondiale du GPS, ce qui suppose d'avoir au moins quatre satellites visibles du sol partout dans le monde. Il y a toujours plus de satellites en orbite afin de maintenir ces 24 emplacements complets même en cas de panne. Depuis 2011, la configuration de la constellation principale est augmentée à 27 emplacements afin de fournir une meilleure couverture mondiale[7]. Les satellites évoluent sur six plans orbitaux ayant une inclinaison d'environ 55° sur l'équateur[8]. Ils suivent une orbite quasi-circulaire de rayon 26 600 km environ (soit une altitude de 20 200 km) qu'ils parcourent en 11 h 58 min 2 s, soit un demi-jour sidéral. Ainsi, les satellites, vus du sol, reprennent la même position dans le ciel au bout d'un jour sidéral.
| Satellites | Nombre |
|---|---|
| Bloc IIA | 0 |
| Bloc IIR | 12 |
| Bloc IIR(M) | 7 |
| Bloc IIF | 12 |
| Bloc III | 0 |
| Total | 31 |
Les générations successives de satellites sont désignées sous le nom de « Blocs » :
Bloc I : les satellites du Bloc I sont les 11 premiers satellites du système, mis en orbite entre 1978 et 1985, fabriqués par Rockwell International, ils étaient prévus pour une mission moyenne de 4,5 ans et une durée de vie de cinq ans, mais leur durée de vie moyenne s'éleva à 8,76 années ; l'un d'entre eux est même resté pendant 10 ans en activité. Leur mission principale était de valider les différents concepts du GPS. Aujourd'hui, les satellites du Bloc I ne sont plus en service ;
Bloc II : les satellites du Bloc II sont les premiers satellites opérationnels du GPS. De nombreuses améliorations ont été apportées à ces satellites par rapport à la version précédente, notamment en ce qui concerne leur autonomie. Ils sont capables de rester 14 jours sans contact avec le segment sol tout en gardant une précision suffisante. Neuf satellites furent lancés en 1989 et 1990. Bien qu'on ait estimé leur durée de vie à 7,5 ans, la plupart d'entre eux sont restés en fonction pendant plus de dix ans. Il ne reste plus de satellite du Bloc II actif ;
Bloc IIA : les satellites du Bloc IIA, au nombre de 19 et lancés entre 1990 et 1997, correspondent à une version perfectionnée des satellites du Bloc II initial. Ils sont équipés de deux horloges atomiques au césium et de deux horloges au rubidium. Ils ont marqué à partir de 1993 le début de la phase opérationnelle du GPS. Début 2016, le dernier satellite du Bloc IIA a cessé de fonctionner après 25 ans de service[9] ;
Bloc IIR : les satellites du Bloc IIR sont dotés d'une meilleure autonomie, fabriqués par Lockheed Martin Corporation, et mis en orbite entre 1997 et 2009, ils peuvent se transmettre mutuellement des messages sans aucun contact au sol, permettant ainsi aux opérateurs du système de pouvoir communiquer avec des satellites qui leur sont inaccessibles dans une communication directe. Ils sont équipés de trois horloges atomiques au rubidium. Vingt-et-un satellites du Bloc IIR ont été lancés, le dernier le 17 août 2009. Les huit derniers sont désignés sous le sigle IIR-M parce qu'ils émettent un nouveau code civil (L2C) sur la fréquence L2 et de nouveaux codes militaires (M) sur les fréquences L1 et L2. Le satellite IIR-M7 a été modifié pour émettre le nouveau signal sur la fréquence L5, implanté sur les satellites du Bloc IIF[note 1] ;
Bloc IIF : les satellites du Bloc IIF (Follow-On) construits par Boeing sont au nombre de 12, le premier de la série a été lancé en mai 2010, le dernier en février 2016. Ces satellites émettent un nouveau signal civil sur la fréquence L5 ;
Bloc III : les 10 premiers satellites du Bloc III seront construits par Lockheed Martin Corporation. Ils émettront un nouveau signal civil (L1C) sur la fréquence L1. Le premier satellite du bloc III a été lancé le 23 décembre 2018[10].

Satellite GPS non lancé exposé au San Diego Aerospace Museum
Segment de contrôle |
C'est la partie qui permet de piloter et de surveiller le système. Il est composé de cinq stations au sol du 50th Space Wing de l'Air Force Space Command, basé à la Schriever Air Force Base dans le Colorado (la station maîtresse est basée à Colorado Springs) dans la base de Cheyenne Mountain. Leur rôle est de mettre à jour les informations transmises par les satellites (éphémérides, paramètres d'horloge) et contrôler leur bon fonctionnement.

Trois récepteurs GPS
Segment utilisateur |
Le segment utilisateur regroupe l'ensemble des récepteurs GPS militaires et civils qui reçoivent et exploitent les signaux des satellites GPS pour calculer des données de position, de vitesse ou de temps[11]. Comme les utilisateurs ne font que recevoir (ils n'émettent pas vers les satellites), le système ne peut être saturé et le nombre maximum d'utilisateurs GPS est illimité.
En 2014, le nombre total de récepteur GPS est estimé à 3,6 milliards[note 2]. Les smartphones avec GPS intégré sont les plus nombreux avec 3,08 milliards, suivi par les 260 millions d'assistants de navigation pour des applications routières. Le nombre restant d'appareils est réparti entre des applications variées : autres transports (aviation, ferroviaire, maritime), topographie, agriculture, infrastructure critique[12].
Principe de fonctionnement |
Le GPS fonctionne grâce au calcul de la distance qui sépare un récepteur GPS de plusieurs satellites. Les informations nécessaires au calcul de la position des satellites étant transmises régulièrement au récepteur, celui-ci peut, grâce à la connaissance de la distance qui le sépare des satellites, connaître ses coordonnées.
Signal émis |

Schéma du signal C/A
Les satellites GPS émettent plusieurs signaux codés, à destination civile ou militaire. Le signal civil pour l'utilisation libre correspond au code C/A, émis sur la porteuse de 1 575 MHz.
Sur cette porteuse, le signal de modulation est une séquence résultant de l'addition modulo 2 du code pseudo-aléatoire C/A à 1 Mbit/s et des données à 50 bit/s contenant les éphémérides des satellites et d'autres informations de navigation. C'est le code C/A qui sert dans les récepteurs par corrélation avec le signal reçu à déterminer l'instant exact d'émission de celui-ci.
Cet instant d'émission de référence du code C/A peut être modulé, à nouveau par un code pseudo-aléatoire, pour dégrader la détermination de position au sol. Ce chiffrement est appelé « selective availability (en) » (SA), faisant passer la précision du système de 10 m environ à 100 m. Il a été abandonné en 2000 sous la pression des utilisateurs civils, et en raison du développement du DGPS qui le compensait en grande partie. Cette possibilité est cependant toujours présente à bord des satellites. La SA comporte aussi la possibilité de dégrader les informations permettant de calculer la position des satellites sur leur orbite ; elle n'a jamais été utilisée.
Mesure de la distance du récepteur par rapport à un satellite |
Les satellites envoient des ondes électromagnétiques (micro-ondes) qui se propagent à la vitesse de la lumière. Connaissant celle-ci, on peut alors calculer la distance qui sépare le satellite du récepteur en connaissant le temps que l'onde a mis pour parcourir ce trajet.
Pour mesurer le temps mis par l'onde pour lui parvenir, le récepteur GPS compare l'heure d'émission - incluse dans le signal - à l'heure de réception de l'onde par le récepteur. Cette mesure, après multiplication par la vitesse du signal, fournit une pseudo-distance, assimilable à une distance, mais entachée d'une erreur de synchronisation des horloges du satellite et du récepteur, et de dégradations comme celles dues à la traversée de l'atmosphère. L'erreur d'horloge peut être modélisée sur une période assez courte à partir des mesures sur plusieurs satellites.
Calcul de la position |
Connaissant les positions des satellites à l'heure d'émission des signaux, et les pseudo-distances mesurées (éventuellement corrigées de divers facteurs liés notamment à la propagation des ondes), le calculateur du récepteur est en mesure de résoudre un système d'équations dont les quatre inconnues sont la position du récepteur (trois inconnues) et le décalage de son horloge par rapport au temps GPS. Ce calcul est possible dès que l'on dispose des mesures relatives à quatre satellites ; un calcul en mode dégradé est possible avec trois satellites seulement si l'on connaît l'altitude ; lorsque plus de quatre satellites sont visibles (ce qui est très souvent le cas), le système d'équations à résoudre est surabondant : la précision du calcul est améliorée, et on peut estimer les erreurs sur la position et le temps.
La précision de la position obtenue dépend, toutes choses égales par ailleurs, de la géométrie du système : si les satellites visibles se trouvent tous dans un cône d'observation de faible ouverture angulaire, la précision sera moins bonne que s'ils sont répartis régulièrement dans un large cône. Les effets de la géométrie du système de mesure sur la précision sont décrits par un paramètre : le DOP (pour « Dilution of Precision », en français « atténuation » ou « diminution de la précision ») : le HDOP se réfère à la précision horizontale, le TDOP à la précision sur le temps, le VDOP à la précision sur l'altitude. La précision espérée est d'autant meilleure que le DOP est petit.
|
La résolution de l'équation de navigation peut se faire par la méthode des moindres carrés et la méthode de Bancroft[13]. Elle nécessite quatre équations (4 satellites).
Chaque signal satellite donne au récepteur l'équation suivante :
ρi=c⋅(tri−tei)=(xi−x)2+(yi−y)2+(zi−z)2+cΔt{displaystyle rho _{i}=ccdot left(t_{r_{i}}-t_{e_{i}}right)={sqrt {left(x_{i}-xright)^{2}+left(y_{i}-yright)^{2}+left(z_{i}-zright)^{2}}}+cDelta t}
avec :
ρi{displaystyle rho _{i}}la distance théorique (i.e. pour une synchronisation parfaite de l'horloge interne du récepteur, soit Δt=0{displaystyle Delta t=0}
) au satellite i{displaystyle i}
;
(xi,yi,zi){displaystyle left(x_{i},y_{i},z_{i}right)}la position du satellite i{displaystyle i}
;
(x,y,z){displaystyle left(x,y,zright)}la position du récepteur;
c{displaystyle c}la vitesse de la lumière dans le vide;
Δt{displaystyle Delta t}le décalage de l'horloge interne du récepteur (le récepteur ne dispose pas d'horloge interne assez précise);
tri{displaystyle t_{r_{i}}}le temps de réception du signal émis à tei{displaystyle t_{e_{i}}}
par le satellite i{displaystyle i}
.
En passant au carré, on obtient :
(ρi−cΔt)2=(xi−x)2+(yi−y)2+(zi−z)2{displaystyle left(rho _{i}-cDelta tright)^{2}=left(x_{i}-xright)^{2}+left(y_{i}-yright)^{2}+left(z_{i}-zright)^{2}}
Puis en développant :
(xi2+yi2+zi2−ρi2)−2(xix+yiy+ziz−ρicΔt)+(x2+y2+z2−(cΔt)2)=0{displaystyle left(x_{i}^{2}+y_{i}^{2}+z_{i}^{2}-rho _{i}^{2}right)-2left(x_{i}x+y_{i}y+z_{i}z-rho _{i}cDelta tright)+left(x^{2}+y^{2}+z^{2}-left(cDelta tright)^{2}right)=0}
On peut alors introduire si=[xiyiziρi]⊤{displaystyle mathbf {s} _{i}=left[{begin{array}{cccc}x_{i}&y_{i}&z_{i}&rho _{i}end{array}}right]^{top }}![{mathbf {s}}_{{i}}=left[{begin{array}{cccc}x_{{i}}&y_{{i}}&z_{{i}}&rho _{{i}}end{array}}right]^{{top }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/af819859164ad12d4c841c87e89bca056b651d2e)
![{mathbf {u}}=left[{begin{array}{cccc}x&y&z&cDelta tend{array}}right]^{{top }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9bc9bcc7a64e43a03ec1c2afbf1cb8303ccbfef9)



12⟨si,si⟩−⟨si,u⟩+12⟨u,u⟩=0{displaystyle {frac {1}{2}}leftlangle mathbf {s} _{i},mathbf {s} _{i}rightrangle -leftlangle mathbf {s} _{i},mathbf {u} rightrangle +{frac {1}{2}}leftlangle mathbf {u} ,mathbf {u} rightrangle =0}
En mettant sous forme matricielle tous les signaux dont on dispose, on obtient :
Bu=a+Λe{displaystyle Bmathbf {u} =mathbf {a} +Lambda mathbf {e} }
avec :
- a=12(⟨s1,s1⟩⟨s2,s2⟩⋮){displaystyle mathbf {a} ={frac {1}{2}}left({begin{array}{c}leftlangle mathbf {s} _{1},mathbf {s} _{1}rightrangle \leftlangle mathbf {s} _{2},mathbf {s} _{2}rightrangle \vdots end{array}}right)}
- B=(x1y1z1−ρ1x2y2z2−ρ2⋮⋮⋮⋮){displaystyle B=left({begin{array}{cccc}x_{1}&y_{1}&z_{1}&-rho _{1}\x_{2}&y_{2}&z_{2}&-rho _{2}\vdots &vdots &vdots &vdots end{array}}right)}
- Λ=12⟨u,u⟩{displaystyle Lambda ={frac {1}{2}}leftlangle mathbf {u} ,mathbf {u} rightrangle }
- e=[11⋯]⊤{displaystyle mathbf {e} =left[{begin{array}{ccc}1&1&cdots end{array}}right]^{top }}
Remarque : le nombre de lignes de a{displaystyle mathbf {a} }


En considérant Λ{displaystyle Lambda }
u⋆=B+(a+Λe){displaystyle mathbf {u} ^{star }=B^{+}left(mathbf {a} +Lambda mathbf {e} right)}

On peut ensuite utiliser Λ=12⟨u,u⟩=12⟨B+(a+Λe),B+(a+Λe)⟩{displaystyle Lambda ={frac {1}{2}}leftlangle mathbf {u} ,mathbf {u} rightrangle ={frac {1}{2}}leftlangle B^{+}left(mathbf {a} +Lambda mathbf {e} right),B^{+}left(mathbf {a} +Lambda mathbf {e} right)rightrangle }
Λ2⟨B+e,B+e⟩+2Λ(⟨B+a,B+e⟩−1)+⟨B+a,B+a⟩=0{displaystyle Lambda ^{2}leftlangle B^{+}mathbf {e} ,B^{+}mathbf {e} rightrangle +2Lambda left(leftlangle B^{+}mathbf {a} ,B^{+}mathbf {e} rightrangle -1right)+leftlangle B^{+}mathbf {a} ,B^{+}mathbf {a} rightrangle =0}
Décalage de l'horloge du récepteur |
La difficulté est de synchroniser les horloges des satellites et celle du récepteur. Une erreur d'un millionième de seconde provoque une erreur de 300 mètres sur la position. Le récepteur ne peut bien entendu pas bénéficier d'une horloge atomique comme les satellites ; il doit néanmoins disposer d'une horloge assez stable, mais dont l'heure n'est a priori pas synchronisée avec celle des satellites. Les signaux de quatre satellites au moins sont nécessaires pour déterminer ce décalage, puisqu'il faut résoudre un système d'au moins quatre équations mathématiques à quatre inconnues qui sont la position dans les trois dimensions plus le décalage de l'horloge du récepteur avec l'heure GPS (voir ci-dessus).
Erreurs possibles |
La plupart des récepteurs sont capables d'affiner leurs calculs en utilisant plus de quatre satellites (ce qui rend les résultats des calculs plus précis) tout en ôtant les sources qui semblent peu fiables, ou trop proches l'une de l'autre pour fournir une mesure correcte, comme précisé ci-dessus.
Cependant, le GPS n'est pas utilisable dans toutes les situations. En particulier la géolocalisation par GPS est quasiment impossible à l'intérieur des bâtiments. Les smartphones, par exemple, capables de se géolocaliser en intérieur n'utlisent pas le positionnement GPS dans ces conditions particulières mais les différents réseaux WIFI disponibles pour ce faire. Le signal émis par les satellites NAVSTAR étant assez faible et différents facteurs peuvent affecter la précision de la localisation : la traversée des couches de l'atmosphère avec entre autres la présence de gouttes d'eau, les simples feuilles des arbres peuvent absorber tout ou partie du signal, et l'« effet canyon » particulièrement sensible dans les gorges, en montagne (d'où son nom) ou en milieu urbain (phénomène de canyon urbain (en)). Il consiste en l'occultation d'un satellite par le relief (un bâtiment par exemple) ; ou pire encore, en un écho du signal contre une surface qui n'empêchera pas la localisation mais fournira une localisation fausse : c'est le problème des multi-trajets des signaux GPS[14].
D'autres erreurs, n'ayant pas de corrélation avec le milieu de prise de mesure ni la nature atmosphérique, peuvent être présentes. Ce sont des erreurs systématiques, telles les décalages orbitaux ou encore un retard dans l'horloge atomique qui calcule le temps auquel la mesure est prise. Un mauvais étalonnage du récepteur (ou autres appareils électroniques du système) peut aussi produire une erreur de mesure[14].
Corrections troposphérique et ionosphérique |
En l'absence d'obstacles, il reste cependant des facteurs de perturbation importants nécessitant une correction des résultats de calcul. Le premier est la traversée des couches basses de l'atmosphère, la troposphère. La présence d'humidité et les modifications de pression de la troposphère modifient l'indice de réfraction n et donc la vitesse et la direction de propagation du signal radio. Si le terme hydrostatique est actuellement bien connu, les perturbations dues à l'humidité nécessitent, pour être corrigées, la mesure du profil exact de vapeur d'eau en fonction de l'altitude, une information difficilement collectable, sauf par des moyens extrêmement onéreux comme les lidars, qui ne donnent que des résultats parcellaires. Les récepteurs courants intègrent un modèle de correction.
Le deuxième facteur de perturbation est l'ionosphère. Cette couche ionisée par le rayonnement solaire modifie la vitesse de propagation du signal. La plupart des récepteurs intègrent un algorithme de correction, mais en période de forte activité solaire, cette correction n'est plus assez précise. Pour corriger plus finement cet effet, certains récepteurs bi-fréquences utilisent le fait que les deux fréquences L1 et L2 du signal GPS ne sont pas affectées de la même façon et recalculent ainsi la perturbation réelle.
En 2017, 16 années de données de perturbation du systèmes GPS par le rayonnement solaire, enregistrées[15] par une constellation de 23 satellites, ont été ouvertes aux scientifiques de la météorologie par le Laboratoire national de Los Alamos (Nouveau-Mexique)[16].
Amélioration locale du calcul |
DGPS |
Le GPS différentiel (Differential global positioning system : DGPS) permet d'améliorer la précision du GPS en réduisant la marge d'erreur du système.
SBAS |
Des systèmes complémentaires d'amélioration de la précision et de l'intégrité ont été déployés (SBAS, Satellite based augmentation system) comme WAAS en Amérique du Nord, MSAS au Japon, EGNOS en Europe ou GAGAN en Inde. Ils reposent tous sur le même principe : un réseau régional ou continental de stations au sol, une ou plusieurs stations maîtres qui centralisent les données des stations et transmettent aux satellites géostationnaires qui rediffusent vers le sol les informations permettant d'améliorer la fiabilité et la précision des données du GPS et d'alerter l'utilisateur en cas de défaillance d'un des satellites.
D'autres pays préparent le déploiement d'un système SBAS : le SDCM pour la Fédération de Russie, le BDSBAS pour la Chine et le K-SBAS pour la Corée du Sud.
Conversion des informations obtenues |
Positionnement |
Les coordonnées terrestre du récepteur sont calculées dans un repère cartésien géocentrique à trois axes (X,Y,Z) qui a pour origine le centre de gravité des masses terrestres (système dit système géodésique). Pour que ces coordonnées soient facilement exploitables, il faut les convertir en coordonnées géographiques (latitude, longitude, altitude), système très largement utilisé en représentation cartographique[17]
C'est le post-traitement du récepteur GPS qui effectue cette conversion en utilisant par défaut le système géodésique WGS 84 (World Geodetic System 84). Ce système, le plus utilisé dans le monde, constitue une référence répondant aux objectifs du système mondial de navigation. L'altitude n'est pas toujours directement exploitable, du fait de l'écart entre la hauteur ellipsoïdale calculé dans le système géodésique WGS 84 et l'altitude géodésique[18]. Cette variation peut atteindre localement plusieurs dizaines de mètres[19],[17] .Les récepteurs les plus élaborés disposent de modèles de correction géodésique, et indiquent une altitude similaire à celle des cartes. Les coordonnées obtenues peuvent être exprimées dans d'autres systèmes géodésiques, propres par exemple à une région ou un pays, ou dans un autre système de projection cartographique. En France, le système de référence est encore souvent la NTF, bien que le système géodésique officiel soit désormais le RGF93, qui diffère très peu du WGS 84.
Temps et synchronisation |
Le calcul des coordonnées géographiques nécessite le calcul du décalage de l'horloge interne du récepteur avec le "temps GPS" et donc le décalage avec le temps UTC. L'horloge du récepteur est synchronisée à celles des satellites à cent milliardièmes de seconde près[20]. Cet accès très précis au temps UTC permet d'asservir très précisément en fréquence une horloge extérieure ou de synchroniser des horloges distantes. Cette possibilité est largement exploitée dans le monde scientifique. Par exemple, l'intégration du temps GPS aux réseaux de surveillance sismique permet aux chercheurs de localiser rapidement l'épicentre des tremblements de terre et d'autres phénomènes telluriques. Dans le monde des transmissions, les grands réseaux de télécommunications nécessitent les équipements parfaitement synchronisés pour fonctionner correctement. les réseaux de téléphonie mobile et de données se servent du temps GPS pour assurer la parfaite synchronisation de toutes leurs stations de base[20].
Visualisation cartographique |
Les récepteurs GPS terrestre ou les smartphones disposant d'une puce GPS incorporent généralement un module de post-traitement disposant des fonctions de visualisation cartographique. Ces fonctions reposent sur des bases de données géographiques intégrées. Elles s'appuient sur l'utilisation de la théorie mathématique des graphes (nœuds) et sur l'utilisation d'algorithmes tel que Gps-less location, Floyd-Warshall, Dijkstra et permettent, par exemple, de déterminer l'itinéraire le plus court entre deux points. La firme Broadcom annonce pour 2018 la sortie d'une puce GPS affichant la position avec une précision de 30 centimètres[21].
Des cartographies peuvent être embarquées dans des Récepteur GPS.
GPS et théorie de la relativité |
Le GPS est l'application concrète la plus courante dont le fonctionnement met en jeu la théorie de la relativité[22],[23]. Si ses effets n'étaient pas pris en compte, la navigation par GPS serait entachée d'erreurs trop importantes[24].
Deux effets principaux de la relativité sont à considérer : la dilatation du temps issue de la relativité restreinte affirme que le temps s'écoule plus lentement pour un objet se déplaçant à grande vitesse, tandis que la relativité générale stipule que le temps s'écoule plus rapidement pour un objet situé plus haut dans un même champ gravitationnel.
Ces deux effets expliquent que la même horloge atomique n'a pas la même fréquence au sol ou en orbite. Pour l'horloge d'un satellite GPS, les deux effets sont contraires : se déplaçant à une grande vitesse son temps est ralenti de 7 μs (7 microsecondes) par jour, alors que située plus haut dans le champ gravitationnel terrestre son temps est accéléré de 45 μs (45 microsecondes) par jour (voir calcul en Tests expérimentaux de la relativité générale). La somme des deux fait que le temps de l'horloge d'un satellite GPS vue du sol avance de δt = 38 μs (38 microsecondes) par jour[22]. Cela correspond donc à une erreur spatiale de δt × c où c est la vitesse de la lumière et donc une dérive de 38 μs × 3 × 108 m/s = 11,4 km/jour.
Historiquement, en 1977, lors de la première mise en orbite d'une horloge atomique au Césium dans le satellite NTS-2, les effets de la relativité avaient été calculés, mais certains doutaient de la véracité des effets relativistes[25]. Les premières émissions du satellite n'incorporaient pas les corrections relativistes, mais il avait été prévu un synthétiseur de fréquence activable à distance qui pourrait le faire. Après vingt jours en orbite, l'horloge atomique en orbite a été mesurée dérivant de 4,425 × 10−10 par rapport au sol[note 3], ce qui était proche du calcul théorique de l'époque donnant 4,465 × 10−10. Par la suite, le synthétiseur a été activé de manière permanente[25]. La valeur de la dérive peut paraître faible, mais elle est bien plus importante que la précision d'une horloge atomique au Césium qui est de l'ordre de 5 × 10−14[26].
Ce décalage est depuis pris en compte dans toutes les horloges atomiques des satellites GPS sous différentes formes. Pour les horloges au Césium, la correction est réalisée au sol avant la mise en orbite. Le cas des horloges atomiques au Rubidium est plus complexe, car elles peuvent subir des sauts de fréquence imprédictibles pendant le lancement. La fréquence est mesurée une fois en orbite, mais elle n'est plus corrigée directement : les corrections nécessaires sont incluses dans le message de navigation[25]. D'autres effets relativistes existent dans le GPS. Certains sont négligeables au vu de la précision recherchée pour les applications de positionnement, d'autres doivent être pris en compte : par exemple, les récepteurs GPS corrigent l'effet Sagnac dû à la rotation de la Terre[27].
Inconvénients du GPS |
Dépendance stratégique |
Le GPS est un système conçu par et pour l'armée des États-Unis et sous son contrôle. Le signal pourrait être dégradé, occasionnant ainsi une perte importante de sa précision, si le gouvernement des États-Unis le désirait. C'est un des arguments en faveur de la mise en place du système européen Galileo qui est, lui, civil et dont la précision théorique est supérieure. La qualité du signal du GPS a été dégradée volontairement par les États-Unis jusqu'au mois de mai 2000, la précision d'un GPS en mode autonome était alors d'environ 100 mètres. Depuis l'arrêt de ce brouillage volontaire, supprimé par le président Bill Clinton, la précision est de l'ordre de 5 à 15 mètres.
Le système GPS est fréquemment utilisé pour la synchronisation de l'heure entre les différents composants des réseaux de téléphonie mobile GSM, UMTS et LTE ; les conséquences d'une dégradation du signal se répercuterait sur une infrastructure critique[28].
Limitations des récepteurs civils |
Les récepteurs GPS civils sont limités afin qu'ils ne puissent pas être utilisés dans des systèmes d'armement rapides tels que les missiles balistiques. En pratique, un récepteur ne doit plus fournir de données de navigation au-delà d'un maximum de vitesse ou d'altitude[29].
Historiquement, ces limites étaient fixées à une vitesse maximale de 515 m/s (1 000 nœuds) et une altitude maximale de 18 000 m (60 000 pieds)[30].
Elles étaient appelées "limites CoCom"[31] du nom du Coordinating Committee for Multilateral Export Controls (CoCom), qui a été dissous après la chute du bloc soviétique en 1994. Par la suite, les réglementations sur les récepteurs GPS sont restées en vigueur aux États-Unis selon l'International Traffic in Arms Regulations (ITAR) qui régule les exportations de technologies sensibles américaines[30] et internationalement selon le Régime de contrôle de la technologie des missiles (MTCR) créé en 1987[32].
Depuis 2013, le MTCR ne limite plus le domaine d'utilisation des GPS civils en altitude et a augmenté la limite de vitesse à 600 m/s [33]. Depuis 2014, les restrictions ITAR aux États-Unis appliquent la même limite[34].
Risque de surveillance abusive |
Dans l'esprit du grand public, un lien direct est effectué entre GPS et surveillance abusive, le terme familier péjoratif de « flicage » est généralement employé par les détracteurs de tels systèmes. Toutefois, les outils de surveillance n'incorporent le GPS que comme l'un des éléments technologiques nécessaires à la surveillance abusive.
Le dispositif de localisation GPS en lui-même est un système passif qui se contente de recevoir les signaux des satellites et d'en déduire une position. Le réseau des satellites GPS ne reçoit donc aucune information d'éventuels systèmes de surveillance au sol (ou embarqués dans un aéronef ou un navire) et demeure techniquement incapable d'effectuer la surveillance d'un territoire d'une quelconque façon.
En revanche, notamment dans le domaine des transports, des systèmes déployés dans les véhicules adjoignent un dispositif de transmission de l'information obtenue avec le GPS. Ce dispositif peut fonctionner en temps réel, il s'agit alors bien souvent d'une liaison de transmission de données par téléphonie mobile ; ou fonctionner en temps différé, les données sont alors déchargées a posteriori par un système physique ou de radio à courte portée. Leur application est généralement réservée aux professionnels pour suivre une flotte de camions, véhicules de transports de passagers (y compris les taxis), de véhicules de commerciaux, de dépannage ou d'intervention. Les objectifs de ces outils de suivi de flotte sont pour un employeur de s'assurer que son salarié effectue effectivement le travail demandé ou que le véhicule n'a pas été détourné. Il permet aussi d'améliorer la gestion d'une flotte de véhicules.
Les individus peuvent également faire l'objet d'une géolocalisation en continu . Il existe deux méthodes de collecte d'informations :
- le tracking ;
- la localisation sous demande.
La première va identifier et remonter l'information à une période constante, par exemple toutes les deux ou cinq minutes. Tandis que la localisation sous demande consiste à n'envoyer l'information qu'en cas de demande du porteur du terminal ou de l'aidant. Dans tous les cas, le porteur du terminal doit être informé et d'accord sur la fonctionnalité de géolocalisation.
Les systèmes de localisation automatique de sécurité, comme l'AIS en navigation maritime et aérienne, combinent un récepteur GPS et un émetteur, améliorant la sécurité anti-collision et la recherche des naufragés. L'APRS utilise le même principe, il est géré par des radioamateurs bénévoles.
Confiance exagérée dans ses performances |
Autres systèmes de positionnement par satellites |
Il existe d'autres systèmes de positionnement par satellite, sans atteindre cependant la couverture ou la précision du GPS :
GLONASS est le système russe, qui est de nouveau pleinement opérationnel depuis décembre 2011 ;
Beidou est le système de positionnement créé par la République populaire de Chine ; il est opérationnel uniquement sur le territoire chinois et les régions limitrophes (il utilise des satellites géostationnaires, au nombre de quatre actuellement) ; son successeur Compass sera global et atteindra une précision de 10 m au sol ;- l'Inde prépare également son système de positionnement, l'IRNSS ;
Galileo est le système civil de l'Union européenne, partiellement opérationnel depuis fin 2016. À terme (prévu vers 2020), il est destiné à être au moins équivalent au GPS en termes de couverture et de précision ;- Le Japon prépare le système QZSS (Quasi-Zenith Satellite System) pour 2017-2018.
Notes et références |
Notes |
Les signaux L1 et L2 de ce satellite sont en 2011 inutilisables à cause d'une interférence entre ces signaux et la charge utile L5.
L'estimation porte sur le nombre total de récepteurs GNSS. La source indique (page 15) que 100 % des appareils incluent la réception du GPS et parfois, en plus, d'autres systèmes de navigation par satellite.
. L'unité de la dérive d'une horloge s'exprime en s/s : ici la dérive est de 4,425 × 10−10 seconde par seconde, soit 0,425 ppb.
Références |
Philippe Béguyot, Bruno Chevalier et Hana Rothova, Le GPS en agriculture : Principes, applications et essais comparatifs, Educagri, 2004, 135 p. (ISBN 2-84444-310-9, lire en ligne), p. 19-26
(en) Bill Clinton, « President Clinton: Improving the Civilian Global Positioning System (GPS) », NARA, 1er mai 2000(consulté le 5 juin 2010)
(en) « EGM96 - The NASA GSFC and NIMA Joint Geopotential Model », NASA, 18 novembre 2004(consulté le 5 juin 2010)
(en) « NGA EGM96 Geoid Calculator », NGA, 16 juin 2006(consulté le 5 juin 2010)
Karen Jego et Victor Battaggion, « Le GPS », Historia, novembre 2011, p. 122 (ISSN 0750-0475)
« Le GPS : une précision toute relativiste », sur www-irma.u-strasbg.fr (consulté le 1er août 2017)
(en) « Space segment », sur http://www.gps.gov/ (consulté le 14 février 2016)
Correia 2012, p. 18
(en) « Last Block IIF to replace oldest GPS satellite », sur http://gpsworld.com/ (consulté le 14 février 2016)
VWilson, « GPS III Space Vehicle 01 Mission », sur SpaceX, 23 décembre 2018(consulté le 30 décembre 2018)
Correia 2012, p. 23
(en) European GNSS Agency, GNSS Market Report, mai 2015, 4e éd., 81 p. (ISBN 978-92-9206-013-8, lire en ligne), p. 8
(en) S. Bancroft, An algebraic solution of the GPS equations, IEEE Transactions on Aerospace and Electronic Systems 21 (1985) p. 56–59
Correia 2012, p. 43-44
J. P. Sullivan,
M. R. Carver, R. M. Kippen, R. H. W. Friedel, G. D. Reeves & M. G. Henderson (2017) Energetic Particle Data From the Global Positioning System Constellation ; Qpace Weather ; DOI: 10.1002/2017SW001604 ; 5 février 2017
Voosen p (2017) Los Alamos releases 16 years of GPS solar weather data ; 30 janvier 2017
« Coordonnées », IGN (consulté le 28 février 2015)
Thierry Dudok de Wit, « GPS et localisation par satellites » [PDF], sur cnrs-orleans.fr, 9 octobre 2010
« Le Quasi-Géoïde », IGN (consulté le 28 février 2015)
« Espace-tempse », sur .gps.gov, 2012(consulté le 1er août 2017)
« Smartphones : vers des GPS (beaucoup) plus précis en 2018 », sur zone-numerique.com/, 25 septembre 2017(consulté le 25 septembre 2017)
Gary Dagorn, « Comment la théorie de la relativité d'Einstein a changé nos vies », Le Monde, 27 novembre 2015(lire en ligne)
(en) Richard W. Pogge, « GPS and Relativity » (consulté le 6 mars 2015)
Asbhy 2007, p. 8
Asbhy 2007, p. 16-17
Asbhy 2007, p. 7
Bartolomé Coll, « Relativistic corrections in the GPS » (consulté le 27 février 2016)
(en) Time Synchronization in Telecom Networks - Meinberg.de, consulté le 21 avril 2012.
(en) GAGA-1: CoCom limit for GPS - John Graham-Cumming, Blog.jgc.org, 28 novembre 2010.
(en) U.S. Satellite Export Policy Report Retains GPS Restrictions - Inside GNSS, 20 avril 2012.
(en) COCOM GPS Tracking Limits - Ravtrack.com, 6 octobre 2010.
Le Régime de contrôle de la technologie des missiles - MTCR, consulté le 29 juillet 2015 (voir archive)
(en) MTCR Equipment Software and Technology annex - MTCR, 17 octobre 2013, p. 51 [PDF] (voir archive).
(en) U.S. Eases Export Regulations for GPS Receivers - Inside GNSS, 30 mai 2014.
Voir aussi |
.mw-parser-output .autres-projets ul{margin:0;padding:0}.mw-parser-output .autres-projets li{list-style-type:none;list-style-image:none;margin:0.2em 0;text-indent:0;padding-left:24px;min-height:20px;text-align:left}.mw-parser-output .autres-projets .titre{text-align:center;margin:0.2em 0}.mw-parser-output .autres-projets li a{font-style:italic}
Bibliographie |
- F. Duquenne et al., GPS localisation et navigation par satellites, 2e édition revue et augmentée, Hermes, 2005
- Paul Correia, Guide pratique du GPS, Editions Eyrolles, décembre 2012, 6e éd., 245 p. (ISBN 2212133677)
SHOM, GPS et Navigation maritime, 1996
(en) GPS Modernization sur U.S. Coast Guard Navigation Center
(en) Neil Harper Server-side GPS and assisted-GPS in JavaTM, 2010- (en) Neil ASHBY, « Relativity in the global positioning system », Living Rev. Relativity, vol. 6, juin 2007(ISSN 1433-8351, lire en ligne)
Articles connexes |
- Système de positionnement par satellites
TRANSIT (prédécesseur du système GPS)
Differential Global Positioning System (DGPS)- Constellation de satellites
- Géolocalisation
- GPS (assistant de navigation)
- Récepteur GPS
- Synchronisation GPS
- Système de coordonnées
- Application du GPS en météorologie
Assisted GPS (A-GPS)- European Geostationary Navigation Overlay Service
- GPX (format de fichier)
Liens externes |
Le Système de Positionnement Mondial au service de la planète - GPS.gov
Système de Positionnement Globa - Informations officielles en langue française du gouvernement des États-Unis sur le système de positionnement global (GPS) et sujets connexes.
- Portail des télécommunications
- Portail de la géographie
- Portail de l’astronautique
- Portail de l’aéronautique
- Portail de l’information géographique
- Portail des forces armées des États-Unis
- Portail du monde maritime








![{mathbf {e}}=left[{begin{array}{ccc}1&1&cdots end{array}}right]^{{top }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fb7ac439c3b8ad1bb92a67a8a06960dff011613f)

