Triangle

Un triangle.
En géométrie euclidienne, un triangle est une figure plane, formée par trois points appelés sommets, par les trois segments qui les relient, appelés côtés, délimitant un domaine du plan appelé intérieur.
Lorsque les sommets sont distincts deux à deux, en chaque sommet les côtés délimitent un angle intérieur, d'où vient la dénomination de « triangle ».
Le triangle est aussi le polygone le plus simple qui délimite une portion du plan et sert ainsi d'élément fondamental pour le découpage et l'approximation de surfaces.
De nombreuses constructions géométriques de points, droites et cercles associés à un triangle sont liées par des propriétés qui étaient en bonne part déjà énoncées dans les Éléments d'Euclide, près de 300 ans avant Jésus-Christ. Les relations entre les mesures des angles et les longueurs des côtés sont notamment à l'origine de techniques de calcul de distances par triangulation. Le développement de ces techniques constitue d'ailleurs une branche des mathématiques appelée trigonométrie.

Un triangle équilatéral sphérique trirectangle.
Hors de la géométrie euclidienne, les côtés d'un triangle sont remplacés par des arcs géodésiques et beaucoup de ses propriétés sont modifiées (voir Trigonométrie sphérique).
La forme triangulaire se retrouve dans de nombreux objets, mathématiques ou non, et s'est chargée de symboliques diverses. De nombreux caractères typographiques présentent une telle forme.
Sommaire
1 Description
1.1 Notations
1.2 Premières propriétés
1.2.1 Inégalité triangulaire
1.2.2 Somme des angles
1.3 Cas particuliers
1.4 Aire
1.5 Périmètre
1.6 Relations trigonométriques
2 Utilisations
2.1 Triangulation
2.2 Décomposition de surface
3 Constructions géométriques associées
3.1 Triangle médian
3.2 Médiatrices et centre du cercle circonscrit
3.3 Céviennes
3.3.1 Médianes et centre de gravité
3.3.2 Hauteurs et orthocentre
3.3.3 Bissectrices et centre du cercle inscrit
3.4 Droite et cercle d'Euler
4 Relations
4.1 Triangles isométriques
4.2 Triangles semblables
5 Autres figures relatives
5.1 Symédianes et point de Lemoine
5.2 Point de Fermat
5.3 Points, droite et cercle de Brocard
5.4 Ellipse de Steiner
6 Autres résultats
6.1 Avec des céviennes
6.2 Avec des cercles
7 Généralisations
7.1 Polygones
7.2 En plus grande dimension
8 Histoire
9 Annexes
9.1 Bibliographie
9.2 Articles connexes
10 Notes et références
10.1 Notes
10.2 Références
Description |
Notations |
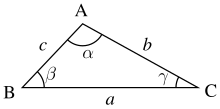
Notations usuelles pour un triangle ABC.
Un triangle est complètement déterminé par la donnée de ses trois sommets et il se note en général en juxtaposant les trois lettres (a priori capitales) qui les désignent. L'ordre de ces lettres importe peu même si l'ordre d'énonciation correspond en général à un parcours dans le sens trigonométrique autour du triangle[1]. La longueur d'un côté est classiquement notée avec la lettre minuscule correspondant au sommet opposé.

dans un triangle ABC.
Si tous les sommets sont distincts[note 1], chaque angle géométrique peut être identifié par la lettre du sommet correspondant, surmontée d'un accent circonflexe. Au cas où la figure comprend d'autres segments passant par les sommets, les côtés de l'angle sont précisés par les lettres désignant les deux autres sommets de part et d'autre sous l'accent circonflexe. Ces angles peuvent aussi être notés à l'aide de lettres grecques en minuscule et en italique.
Premières propriétés |
Inégalité triangulaire |
Le postulat euclidien selon lequel « la ligne droite est le plus court chemin d'un point à un autre » s'illustre par le fait que dans un triangle, la longueur de chaque côté est inférieure à la somme des longueurs des deux autres côtés :
- BC≤BA+AC, AB≤AC+CB et AC≤AB+BC.{displaystyle {rm {BCleq BA+AC,~~ABleq AC+CB~~et~~ACleq AB+BC.}}}
Le cas d'égalité caractérise les triangles plats, dans lequel l'un des sommets appartient au segment qui relie les deux autres.
Réciproquement, étant données trois longueurs (données par trois nombres réels positifs) dont aucune n'est supérieure à la somme des deux autres, il est possible de construire un triangle ayant ces longueurs de côté.
La vérification de ces inégalités peut être faite en comparant seulement la plus grande des trois longueurs avec la somme des deux autres, car les deux autres inégalités sont nécessairement vraies.
Il suffit alors de construire d'abord un segment d'une des trois longueurs souhaitées, puis de tracer deux cercles centrés sur les extrémités de ce segment avec pour rayon chacune des deux autres longueurs. Les deux cercles ont alors deux points d'intersection et n'importe lequel de ces deux points définit le triangle de dimensions voulues avec le segment initial.
Somme des angles |

La somme des mesures des angles d'un triangle vaut 180°.
La somme des angles d'un triangle est égale à un angle plat, autrement dit la somme de leurs mesures vaut 180° (degrés) c'est-à-dire π radians. Cette propriété est une caractéristique de la géométrie euclidienne. Il existe d'autre géométries, dites géométries non euclidiennes, dans lesquelles la somme des angles d'un triangle est toujours supérieure à 180° (on parle alors de géométrie elliptique) ou au contraire inférieure (la géométrie est alors dite géométrie hyperbolique).
Réciproquement, étant données trois mesures (non nulles) d'angles géométriques dont la somme vaut un angle plat, il existe un triangle ayant ces mesures d'angles. Il suffit de tracer un segment d'une longueur quelconque et de tracer une demi-droite en chaque extrémité mais du même côté du segment, de façon à former deux des angles voulus avec le segment initial. Les deux demi-droites auront un point d'intersection en lequel l'angle intérieur sera le troisième angle voulu.
Cas particuliers |
Un triangle dans lequel au moins deux sommets sont confondus est dit dégénéré (ou parfois en aiguille[réf. nécessaire]).
Un triangle plat est un triangle dont les sommets sont alignés.
Un triangle isocèle est un triangle ayant au moins deux côtés de même longueur. Les deux angles adjacents au troisième côté sont alors de même mesure. Réciproquement, tout triangle ayant deux angles de même mesure est isocèle. Les triangles isocèles sont les seuls à admettre un axe de symétrie en dehors des triangles plats. Anciennement, en géométrie euclidienne, un triangle isocèle possédait exactement deux côtés égaux.[réf. nécessaire]
Un triangle équilatéral est un triangle dont les trois côtés ont la même longueur. Ses trois angles ont alors la même mesure qui vaut donc 60° et il admet trois axes de symétrie.
Un triangle qui n'est ni isocèle (ce qui exclut également le cas équilatéral) ni plat est dit scalène (du grec σκαληνός (skalenos) : boiteux, inégal, déséquilibré, oblique…). Un triangle scalène peut aussi être rectangle.
L'adjectif « scalène » n'est pas synonyme de l'adjectif « quelconque ». Un triangle quelconque est un triangle qui peut posséder ou non des propriétés des triangles particuliers. Ainsi un triangle quelconque peut être isocèle ou équilatéral, ou même scalène. Par contre un triangle scalène ne peut être ni équilatéral ni isocèle. L'adjectif « quelconque » est employé pour insister sur le fait qu'on ne sait rien de plus à propos d'un triangle. Dès lors qu'on sait qu'un triangle possède une ou des propriété(s) particulière(s) il ne peut plus être considéré comme quelconque.
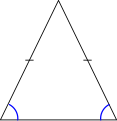
Triangle isocèle.

Triangle équilatéral.
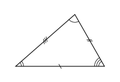
Triangle scalène.
Un triangle rectangle est un triangle ayant un angle droit, c'est-à-dire de mesure 90°. Il satisfait alors le théorème de Pythagore.
Comme la somme des angles d'un triangle vaut 180°, il ne peut y avoir plus d'un angle obtus (supérieur à l'angle droit). S'il y en a un, le triangle est obtusangle ou ambligone. S'il n'y en a pas, il est acutangle ou oxygone (il a alors trois angles aigus).

Triangle obtusangle ou ambligone
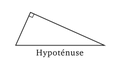
Triangle rectangle

Triangle acutangle ou oxygone
Certains triangles ont reçu une dénomination particulière qui détermine leurs angles :
- le demi-carré est un triangle isocèle rectangle, qui peut s'obtenir en reliant trois sommets d'un carré ;
- le triangle des arpenteurs ou triangle « 3-4-5 » est un triangle rectangle dont les côtés sont de longueurs 3, 4 et 5 en fonction d'une unité fixée ;
- le triangle de l'écolier ou triangle hémi-équilatéral est un triangle rectangle dont les mesures des angles sont de 30°, 60° et 90° ;
- le triangle d'or est un triangle isocèle dont les angles à la base valent deux cinquièmes de l'angle plat, soit 72° ;
- un triangle de Kepler est un triangle rectangle dont les longueurs de côté suivent une progression géométrique.

Demi-carré.
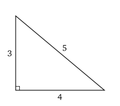
Triangle des arpenteurs.
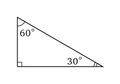
Triangle de l'écolier.
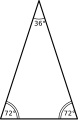
Triangle d'or.
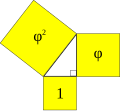
Triangle de Kepler.
Un triangle est dit bisocèle si l'une de ses bissectrices le partage en deux triangles isocèles. Il ne peut s'agir que du demi-carré ou d'un triangle d'or[2].
Le tableau suivant compare quelques un de ces triangles particuliers :
| Triangle | Côtés | Angles |
|---|---|---|
| Équilatéral | Les longueurs des trois côtés sont égales | Les angles sont de 60° |
| Isocèle | Les longueurs de deux côtés sont égales | Les angles adjacents à la base sont égaux |
| Rectangle | Un angle est droit et les deux autres sont inférieurs à 90° | |
| Isocèle rectangle | Les longueurs de deux côtés sont égales | Un angle est droit et les deux autres sont de 45° |
| Obtusangle | Un angle est supérieur à 90° et les deux autres sont inférieurs à 90° | |
| Acutangle | Les trois angles sont inférieurs à 90° |
Aire |
L'aire d'un triangle est donnée par diverses formules, la première étant fonction de la longueur d'un côté, appelée base, et de la distance du sommet opposé à la droite qui porte ce côté, appelée hauteur.
- A=12×base×hauteur.{displaystyle {mathcal {A}}={frac {1}{2}}times mathrm {base} times mathrm {hauteur} .}
Cette formule est dérivée de celle de l'aire d'un parallélogramme et démontrée dans les Éléments d'Euclide.
D'autres formules font appel à la longueur des côtés (formule de Héron) ou aux coordonnées des sommets dans un repère orthonormé.
Périmètre |
Le périmètre d'un triangle est simplement la somme des trois longueurs de côté. Pour un périmètre p donné, l'aire intérieure du triangle est majorée par celle du triangle équilatéral correspondant :
- A≤p2336.{displaystyle {mathcal {A}}leq {frac {p^{2}{sqrt {3}}}{36}}.}
Relations trigonométriques |
Les longueurs de côté d'un triangle et les mesures de ses angles satisfont plusieurs relations qui permettent de toutes les calculer à partir de certaines d'entre elles.
Il s'agit d'une part, outre la formule de la somme des angles, d'une relation entre l'aire, la mesure d'un angle et la longueur des deux côtés adjacents :
- A=12bcsinA^{displaystyle {mathcal {A}}={dfrac {1}{2}}bc,sin {hat {A}}}
laquelle permet d'obtenir la formule des sinus :
asinA^=bsinB^=csinC^=2R{displaystyle {dfrac {a}{sin {hat {A}}}}={dfrac {b}{sin {hat {B}}}}={dfrac {c}{sin {hat {C}}}}=2R}où R est le rayon du cercle circonscrit ;
d'autre part, du théorème d'Al-Kashi (ou théorème de Carnot[réf. nécessaire] ou encore loi des cosinus) qui généralise le théorème de Pythagore :
a2=b2+c2−2bccosA^{displaystyle a^{2}=b^{2}+c^{2}-2bccos {hat {A}}}.
Utilisations |
Triangulation |
Les relations métriques dans le triangle permettent d'évaluer des distances à partir de mesures angulaires, comme en navigation maritime, en géodésie et en astronomie. C'est selon ce principe qu'a été mesuré le méridien terrestre pour la définition du mètre[3].
Décomposition de surface |

Les trois polyèdres réguliers convexes à faces triangulaires
Dans le plan, le calcul de l'aire d'un domaine peut être évalué en approchant ce domaine par une réunion de triangles disjoints.
Plus généralement, des surfaces de l'espace peuvent être approchées par une réunion de triangles appelées facettes. Cette technique est utilisée en analyse numérique dans la méthode des éléments finis, mais aussi en imagerie numérique. L'analyse vectorielle permet d'ailleurs de calculer rapidement l'orientation d'une telle facette et d'en déduire la réflexion du rayonnement lumineux d'une source ponctuelle dans une direction donnée.
Plusieurs polyèdres (réguliers ou non) ont des faces triangulaires, comme le tétraèdre, l'octaèdre, l'icosaèdre et le grand icosaèdre. Les polyèdres dont toutes les faces sont des triangles équilatéraux sont appelés deltaèdres.
D'autre part, tout polygone peut être découpé en un nombre fini de triangles qui forment alors une triangulation de ce polygone. Le nombre minimal de triangles nécessaire à ce découpage est n-2, où n est le nombre de côtés du polygone. L'étude des triangles est fondamentale pour celle des autres polygones, par exemple pour la démonstration du théorème de Pick.
Constructions géométriques associées |
Triangle médian |

Triangle médian, médianes et centre de gravité.
Si on joint les trois milieux des côtés d'un triangle on obtient quatre triangles semblables au triangle initial, l'aire de chacun des triangles est le quart de celle du triangle initial.
On appelle triangle médian le triangle central dont les sommets sont les milieux des côtés du triangle initial. Ce triangle médian se trouve « inversé » par rapport aux trois autres.
D'après le théorème des milieux, ce triangle médian a ses côtés parallèles à ceux du triangle initial et des longueurs de côté proportionnelles dans un rapport de 1/2.
Médiatrices et centre du cercle circonscrit |

Médiatrices et cercle circonscrit.
Si le triangle est non plat, les trois médiatrices des côtés (les droites coupant les côtés à angle droit en leur milieu) sont concourantes en un point appelé centre du cercle circonscrit, car il est le seul équidistant des trois sommets, c'est-à-dire qu'il est le centre du seul cercle passant par les trois sommets. Ce centre est souvent noté O ou Ω (« oméga »).
Un triangle est rectangle si et seulement si le centre de son cercle circonscrit est le milieu de l'un de ses côtés (qui est alors son hypoténuse).
Pour un triangle acutangle, le centre du cercle circonscrit est à l'intérieur du triangle. Pour un triangle obtusangle, ce centre est à l'extérieur.
Le produit du rayon du cercle circonscrit et de l'aire du triangle est le quart du produit des longueurs de côtés du triangle.
Céviennes |
Une cévienne d'un triangle est un segment de droite partant d'un sommet et joignant son côté opposé. Les médianes, hauteurs et bissectrices sont des céviennes particulières.
Médianes et centre de gravité |
Dans un triangle, une médiane est un segment qui relie un sommet au milieu du côté opposé. Chaque médiane divise un triangle en deux triangles d'aires égales.
Si le triangle est non plat, les trois médianes sont concourantes en un point appelé centre de gravité. Ce point, souvent noté G et situé aux deux-tiers de chaque médiane en partant du sommet, est à la fois l'isobarycentre des trois sommets et le centre de masse de l'intérieur du triangle.
Les trois médianes concourantes divisent le triangle en six triangles de même aire.
La longueur de la médiane est reliée aux longueurs des autres côtés par le théorème de la médiane ou théorème d'Apollonius.
Hauteurs et orthocentre |

Hauteurs et orthocentre.
Si les trois sommets sont distincts, une hauteur est une droite passant par un sommet et perpendiculaire au côté opposé. Si le triangle est non plat, les trois hauteurs sont concourantes en un point appelé orthocentre, souvent noté H.
Un triangle est rectangle si et seulement si son orthocentre est l'un des sommets (en lequel se trouve alors l'angle droit).
Pour un triangle acutangle, l'orthocentre est à l'intérieur du triangle. Pour un triangle obtusangle, il est à l'extérieur.
Les trois médiatrices d'un triangle sont les trois hauteurs de son triangle médian et par conséquent, le centre du cercle circonscrit à un triangle est l'orthocentre du triangle médian.
Le point de Longchamps est le symétrique de l'orthocentre par rapport au centre du cercle circonscrit.
Bissectrices et centre du cercle inscrit |

Bissectrices et cercle inscrit.
Si le triangle est non plat, les trois bissectrices de ses angles (les demi-droites qui partagent les angles en deux angles de même mesure) sont concourantes en un point appelé centre du cercle inscrit, car il est le centre du seul cercle tangent aux trois côtés. Ce centre est en général noté I ou J.
D'après le théorème de Steiner-Lehmus, les longueurs de deux bissectrices dans un triangle sont égales si et seulement si les angles correspondants ont même mesure.
Les points de contact de ce cercle inscrit avec les côtés forment le triangle de Gergonne. Les segments reliant ces points de contact avec les sommets opposés dans le triangle sont concourantes en un point appelé point de Gergonne.
Chaque bissectrice divise le côté opposé en deux segments dont les longueurs sont reliées à celles des côtés de l'angle grâce à la loi des sinus.
Le segment de bissectrice , intérieur au triangle , issu du sommet A (par exemple) a pour longueur 2 b c cos(A/2) / (b+c)
Le rayon du cercle inscrit est le quotient de l'aire du triangle par son demi-périmètre.
Droite et cercle d'Euler |

Droite et cercle d'Euler.
Le centre de gravité, le centre du cercle circonscrit et l'orthocentre sont alignés sur une droite appelée droite d'Euler et satisfont la relation vectorielle :
- ΩH→=3ΩG→.{displaystyle {overrightarrow {Omega mathrm {H} }}=3,{overrightarrow {Omega mathrm {G} }}.}
En outre, les milieux des côtés, les pieds des hauteurs et les milieux des segments reliant l'orthocentre aux sommets sont tous sur un même cercle appelé cercle d'Euler, dont le centre est également sur la droite d'Euler.
Particularité : soit M un point de la droite d'Euler . Les cercles d'Euler des triangles AHM , BHM et CHM se recoupent sur le cercle d'Euler du triangle ABC . Si M est le centre du cercle circonscrit au triangle ABC , alors le point de concours est nommé point de Jérabek .
Relations |
Triangles isométriques |
Deux triangles sont dits isométriques, superposables ou, anciennement[4]égaux, s'ils ont les mêmes longueurs de côté. Dans ce cas il est possible de faire correspondre les sommets de l'un avec les sommets de l'autre par une isométrie (par exemple une translation, une rotation ou une symétrie) et cette correspondance relie alors des angles de même mesure. Ces triangles ont donc aussi la même aire.
Cette première définition est équivalente à chacune des trois suivantes :
- les trois longueurs des côtés du premier triangle sont les mêmes que celles du second (abrégé par CCC) ;
- les deux triangles ont un angle de même mesure compris entre deux côtés de mêmes longueurs (abrégé par CAC) ;
- les deux triangles ont un côté de même longueur compris entre deux angles de mêmes mesures (abrégé par ACA).
Triangles semblables |
Deux triangles ayant les mêmes mesures d'angle sont dits semblables. Ils ne sont pas nécessairement isométriques, mais leurs longueurs de côté sont proportionnelles avec un même coefficient de proportionnalité k. Leurs aires sont alors reliées par un facteur k2.
Il existe en effet une similitude (qui est la composée d'une isométrie et d'une homothétie) qui transforme l'un en l'autre. Cette définition équivaut à :
- les trois angles du premier ont mêmes mesures que ceux du second (abrégé par AAA), (en fait deux angles suffisent : le troisième s'en déduit)
ou encore à :
- les trois longueurs des côtés du premier sont proportionnelles à celles du second.
Deux triangles isométriques sont toujours semblables. Deux triangles équilatéraux (non nécessairement isométriques) aussi.
Autres figures relatives |
Il existe trois autres cercles tangents simultanément aux trois droites qui portent les côtés d'un triangle, et sont tous trois extérieurs à ce triangle. Les points d'intersection de ces cercles avec les côtés du triangle forment le triangle de Nagel. Les segments reliant ces points de contact avec les sommets opposés du triangle sont concourants en un point appelé point de Nagel.
Le cercle dont un diamètre relie le point de Nagel à l'orthocentre est appelé cercle de Fuhrmann et son rayon est égal à la distance entre les centres des cercles inscrit et circonscrit.
Les centres des trois cercles forment le triangle de Bevan, qui est homothétique au triangle de Gergonne. Le centre de son cercle circonscrit est appelé point de Bevan.
Les trois cercles exinscrits sont tangents intérieurement à un cercle appelé cercle d'Apollonius. Les droites reliant les points de contact aux sommets opposés du triangle sont concourantes en un point appelé point d'Apollonius.
Le cercle inscrit et les trois cercles exinscrits sont tous tangents au cercle d'Euler. Les points de contact sont appelés points de Feuerbach.
Symédianes et point de Lemoine |
Une symédiane est une droite symétrique de la médiane par rapport à une bissectrice issue du même sommet. Les trois symédianes sont concourantes en un point appelé point de Lemoine.
Point de Fermat |
Dans un triangle acutangle, il existe un unique point qui minimise la somme des distances aux sommets. En ce point, appelé point de Fermat, les angles formés par les segments vers les sommets du triangle sont tous de 120°.
Points, droite et cercle de Brocard |

Points de Brocard
Si un triangle est non plat, il existe deux points appelés points de Brocard pour lesquels les segments vers les sommets subdivisent le triangle en trois triangles ayant un angle de même mesure par permutation des sommets du triangle initial.
La mesure de cet angle est alors la même pour les deux points.
La droite de Brocard est la droite qui passe par ces deux points.
Les points de Brocard appartiennent au cercle de Brocard dont un diamètre a pour extrémités le centre du cercle circonscrit et le point de Lemoine.
D'après le théorème d'Alasia, la droite de Brocard est parallèle à l'un des côtés si et seulement si le triangle est isocèle avec ce côté pour base.
Ellipse de Steiner |
Dans un triangle non plat, il existe une unique ellipse tangente à chaque côté en son milieu.
Autres résultats |
Le théorème de Thalès relie les longueurs de côtés de deux triangles semblables ayant un sommet commun et les côtés opposés parallèles.
Le théorème de Napoléon affirme que les centres des triangles équilatéraux formés extérieurement sur les côtés d'un triangle sont eux-mêmes les sommets d'un triangle équilatéral.
Le « théorème japonais de Carnot » établit que la somme des rayons des cercles inscrit et circonscrit est égale à la somme des distances du centre du cercle circonscrit aux côtés du triangle.
Le théorème de Ménélaüs donne une condition nécessaire et suffisante pour l'alignement de trois points alignés respectivement avec les côtés d'un triangle.
Le théorème de Morley affirme que les intersections des trissectrices des angles d'un triangle forment un triangle équilatéral.
Le théorème de Nagel montre que la bissectrice d'un angle d'un triangle est la même que celle de l'angle en ce sommet dont les côtés passent par l'orthocentre et le centre du cercle circonscrit.
Le théorème de Neuberg établit que les centres de trois carrés obtenus par une construction géométrique particulière sur un triangle sont les milieux des côtés de ce triangle.
Le théorème de Hamilton stipule que le cercle d'Euler est le même pour les quatre triangles formés par un groupe orthocentrique.
Le théorème d'Euler en géométrie exprime la distance d entre les centres des cercles inscrit et circonscrit en fonction de leurs rayons respectifs r et R par d2=R(R-2r). Il en découle que le rayon du cercle inscrit est au moins deux fois plus petit que celui du cercle circonscrit (inégalité d'Euler).
Avec des céviennes |
Le théorème de Ceva donne une condition nécessaire et suffisante pour que trois droites (appelées céviennes) passant respectivement par les trois sommets d'un triangle soient parallèles ou concourantes.
Le théorème de Gergonne donne alors une relation entre les longueurs des céviennes et les longueurs des segments qui relient leur point d'intersection aux sommets.
Le théorème de Stewart relie la longueur d'une cévienne aux longueurs des côtés des deux triangles qu'elle forme.
Le théorème de Terquem montre que le cercle pédal, circonscrit au triangle pédal formé par les trois pieds de céviennes concourantes, coupe les côtés du triangle en trois points qui sont également les pieds de céviennes concourantes.
Le théorème de Routh donne le quotient des surfaces entre l'aire du triangle formé par trois céviennes, et celle d'un triangle donné.
Avec des cercles |
Le théorème des six cercles montre qu'une suite de cercles successivement tangents extérieurement et tangents intérieurement à deux côtés d'un triangle (les côtés variant par permutation circulaire) est 6-périodique.
La réciproque du théorème des trois cercles de Miquel montre que trois cercles passant respectivement par les sommets d'un triangle et sécants le long des côtés correspondants sont concourants en un point appelé point de Miquel.
Généralisations |
Polygones |

Un quadrilatère, avec ses diagonales
Un triangle étant un polygone à trois côtés, certaines propriétés se généralisent pour un plus grand nombre de côtés, comme l'inégalité triangulaire ou la somme des angles (pour un polygone non croisé), mais l'aire et les angles ne dépendent plus seulement des longueurs des côtés. Il y a aussi moins de résultats valables en toute généralité sur les droites ou points remarquables. Cependant, certaines conditions permettent d'en retrouver comme dans le cas de quadrilatères particuliers (parallélogrammes notamment) ou inscriptibles dans un cercle.
En plus grande dimension |

Un tétraèdre
Dans l'espace, trois points sont toujours coplanaires et ne suffisent donc pas pour définir un élément de volume. Mais quatre points non coplanaires forment un tétraèdre. Plus généralement, un simplexe est une figure géométrique convexe engendré par n points dans un espace à au moins n−1 dimensions.
Histoire |

Problèmes R49→R55 du papyrus Rhind

figure du triangle représentée dans le problème R51 du papyrus Rhind
Aucun document mathématique de l'Ancien Empire ne nous est parvenu. Mais l'architecture monumentale des IIIe et IVe dynastie constitue une preuve remarquable que les Égyptiens de cette époque détenaient des connaissances relativement élaborées en géométrie, et en particulier dans l'étude des triangles.
Le calcul de l'aire de cette figure est étudié dans les problèmes R51 du papyrus Rhind, M4, M7 et M17 du papyrus de Moscou et datant tous du Moyen Empire. Le problème R51 constitue, dans l'histoire mondiale des mathématiques, le premier témoignage écrit traitant du calcul de l'aire d'un triangle.
- Énoncé du problème R51 du papyrus Rhind[5]
« Exemple de calcul d'un triangle de terre. Si quelqu'un te dit : un triangle de 10 khet sur son mryt et de 4 khet sur sa base. Quelle est sa superficie ? Calcule la moitié de 4 qui est 2 pour en faire un rectangle. Tu fais en sorte de multiplier 10 par 2. Ceci est sa superficie. »
Le terme mryt signifie probablement hauteur, ou côté. Mais la formule utilisée pour le calcul de l'aire fait pencher l'interprétation en faveur de la première solution[6]. Le scribe prenait la moitié de la base du triangle et calculait l'aire du rectangle formé par ce côté et la hauteur, soit
A=base2mryt{displaystyle A={frac {base}{2}}{mryt}}

équivalente à la formule générale utilisée de nos jours :
S=ah2.{displaystyle S={frac {ah}{2}}.}

Euclide, dans le livre I de ses Éléments, vers 300 av. J.-C., énonce la propriété sur la somme des angles du triangle et les trois cas d'égalité des triangles (voir ci-dessus le paragraphe sur les triangles isométriques).
Annexes |
Bibliographie |
- Arnold Buffum Chace (en), The Rhind Mathematical Papyrus: Free Translation and Commentary with Selected Photographs, Translations, Transliterations and Literal Translations, vol. II, 1927-1929
- Jean-Denis Eiden, Géométrie analytique classique, Calvage & Mounet, 2009 (ISBN 978-2-91-635208-4)
- Marshall Clagett (en), Ancient Egyptian Science, A Source Book, vol. 3 : Ancient Egyptian Mathematics, American Philosophical Society, 1999
Articles connexes |
- Aire de surfaces usuelles
- Nombre triangulaire
- Liste des éléments remarquables d'un triangle
- Résolution d'un triangle
- Triangle de Pascal
- Triangle de Penrose
- Triangle de Sierpiński
- Triangle de Kobon
- Symbolique du triangle
- Triangle (caractère)
Notes et références |
Notes |
Dans le cas où deux sommets sont confondus, la direction du côté qui les relie n'est pas définie et les angles adjacents non plus.
Références |
Stella Baruk, « Triangle », dans Dictionnaire de mathématiques élémentaires [détail des éditions].
Voir la démonstration sur la page triangle au collège.
Histoire des nombres.[réf. non conforme]
Par exemple dans cette traduction des Éléments d'Euclide.
A. Buffum Chace, Rhind papyrus, pl. 73.
Clagett, Ancient Egyptian Science, p. 70.
- Portail de la géométrie
















