Argthtjtr

Pour les articles homonymes, voir Aberration.

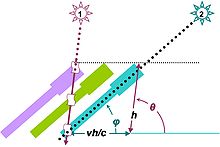
La lumière en provenance de l'endroit 1 semblera provenir de l'endroit 2 pour un télescope en mouvement à cause de la vitesse finie de la lumière, c'est l'aberration de la lumière.

L'aberration de la lumière est un phénomène optique qui se traduit par le fait que la direction apparente d'une source lumineuse dépend de la vitesse de celui qui l'observe (plus exactement de la composante de cette vitesse perpendiculaire à la direction d'observation), de la même façon que pour un passager d'un véhicule qui se déplace par exemple à l'horizontale, la pluie semble tomber depuis une direction située vers l'avant, et non selon la verticale. L'astronome James Bradley découvrit le phénomène en 1725 en étudiant les variations de la position apparente de l'étoile γ Draconis. Il lui fallut près de deux ans avant de comprendre ce phénomène et le publier. Il fournit ainsi la première confirmation scientifique de la rotation de la Terre autour du Soleil par l'observation des étoiles.

Aspects historiques |

La possibilité d'un déplacement apparent des étoiles comme conséquence du modèle copernicien avait été émise dès la fin du XVI^e siècle, mais c'est à un mouvement de parallaxe que la plupart des écrits faisaient allusion. Jusqu'à la fin du XVII^e siècle, aucune mesure fiable ne montre de mouvement apparent d'étoiles. C'est l'astronome français Jean Picard qui semble-t-il a été le premier à observer le phénomène d'aberration en 1680, mais qu'il tenta en vain d'expliquer en termes de parallaxe.

Le phénomène d'aberration de la lumière avait fait l'objet de plusieurs études après que Ole Christensen Rømer eut mesuré pour la première fois la vitesse de la lumière en 1676. Plusieurs tentatives de mise en évidence, notamment par l'astronome britannique John Flamsteed en 1689 eurent lieu. Il fut observé de manière convaincante par Bradley au mois de décembre 1725 avec l'étoile γ Draconis confirmé par ses observations supplémentaires en mars 1726. Plusieurs autres étoiles furent observées en 1727.

Bradley eut beaucoup de difficultés à comprendre ses observations. Une hypothèse qu'il envisagea d'abord était que le mouvement apparent des étoiles était une conséquence d'une variation de l'axe de rotation de la Terre. Cependant cette interprétation ne permettait pas d'expliquer les observations. L'anecdote raconte que c'est en observant la variation de la direction apparente du vent selon la vitesse et la direction prise par un voilier que Bradley eut l'idée d'appliquer ce raisonnement finalement assez simple à la lumière. Après s'être assuré de la validité de l'hypothèse selon laquelle c'était l'aberration qui était responsable du mouvement apparent des étoiles, il se rendit compte qu'en soustrayant ce phénomène aux mouvements apparents observés il subsistait encore un mouvement apparent des étoiles. Se souvenant de son hypothèse initiale, il put alors démontrer l'existence d'une petite variation de l'axe de rotation de la Terre : c'est le phénomène de nutation qu'il ne choisit de publier qu'une vingtaine d'années plus tard en 1748.

Description du phénomène |

Effets de la variation annuelle de l'aberration de la lumière sur la position apparente de trois étoiles à une longitude par rapport à l'écliptique de 270° et à une latitude respectivement de 90°, 45° et 0°.

En pratique, le phénomène d'aberration peut être observé pour les étoiles. On observe un mouvement elliptique apparent de celles-ci au cours d'une année. Ce phénomène est dû à la vitesse relative de la Terre sur son orbite par rapport aux étoiles, et donc aux rayons lumineux qui en proviennent. Il ne dépend pas de la distance de l'étoile à la Terre, mais seulement de l'angle entre sa direction et le plan de l'écliptique (plan de l'orbite terrestre autour du soleil). Il ne doit pas être confondu avec la parallaxe qui est due à un effet de perspective, sensible seulement pour les étoiles assez proches. En outre, les deux phénomènes n'ont pas le même ordre de grandeur, environ 20 secondes d'arc pour l'aberration, contre une seconde d'arc pour la parallaxe des étoiles les plus proches, moins pour les plus éloignées. C'est d'ailleurs cette différence d'ordre de grandeur qui permit la découverte de l'aberration des étoiles, près d'un siècle avant celle de leur parallaxe. Du fait de la rotation de la Terre, il existe également un phénomène d'aberration diurne, d'autant plus prononcé que l'observateur est situé proche de l'Équateur. L'amplitude de ce phénomène est cependant bien plus faible, de l'ordre d'une fraction de seconde d'arc.

Le phénomène d'aberration a apporté la première confirmation scientifique au modèle copernicien^[1]. Il a permis également de montrer que la vitesse de la lumière émise par toutes les étoiles était la même, ne dépendait ni de l'étoile, ni de sa luminosité (mais seulement de sa direction par rapport au plan de l'écliptique). Ainsi il a été possible d'estimer plus précisément cette vitesse, de manière cohérente avec la première estimation faite par Rømer une cinquantaine d'années auparavant. À l'époque, les incertitudes sur la taille du système solaire ne permettaient pas de connaître avec précision la taille de l'orbite de la Terre et par suite sa vitesse de déplacement le long de son orbite, ce qui empêchait une mesure précise de la vitesse de la lumière.

Une conséquence surprenante du phénomène d'aberration est qu'un observateur fortement accéléré atteignant une vitesse proche de celle de la lumière verrait la quasi-totalité des objets situés devant lui projetés vers une direction apparente très proche de la direction vers laquelle il se dirige, lui donnant l'impression erronée qu'il est en train de s'éloigner de la direction vers laquelle il se déplace. Ce phénomène permettrait ainsi à un observateur au mouvement très rapide de voir vers l'avant des objets en fait situés derrière lui.

Calcul classique |

On considère deux référentiels R{displaystyle R} et R′{displaystyle R'} en translation l'un par rapport à l'autre, avec une vitesse relative v selon leurs abscisses respectives. On suppose que les axes des deux référentiels restent parallèles. Si la lumière parvient dans le plan Oxy{displaystyle Oxy} du référentiel R{displaystyle R}, en faisant un angle θ avec l'axe Ox{displaystyle Ox}, la vitesse de la lumière a alors pour composantes (−ccos⁡θ−csin⁡θ){displaystyle {begin{pmatrix}-ccos theta \-csin theta end{pmatrix}}}. Dans le référentiel R′{displaystyle R'}, ces composantes deviennent (−ccos⁡θ−v−csin⁡θ){displaystyle {begin{pmatrix}-ccos theta -v\-csin theta end{pmatrix}}}, formant donc un angle θ′{displaystyle theta '} (ou ϕ{displaystyle phi }, selon la figure) tel que :

tan⁡θ′=sin⁡θcos⁡θ+v/c{displaystyle tan theta '={sin theta over cos theta +v/c}}

Si l'étoile est au zénith (θ=π/2{displaystyle theta =pi /2}), alors tan⁡θ′=cv{displaystyle tan theta '={c over v}} ou encore tan⁡(π/2−θ′)=vc{displaystyle tan(pi /2-theta ')={v over c}}. L'écart d'angle est faible, proche de v/c. L'observation de la même étoile à six mois d'intervalle (pendant lesquels la vitesse de la Terre passe de v à -v dans le référentiel choisi, qui n'a pas tourné) permet de mesurer le double de cet angle. Connaissant v, on peut en déduire c. Pour le phénomène d'aberration des étoiles, c'est le rapport v/c{displaystyle v/c} que l'on mesure, où v{displaystyle v} est la vitesse orbitale de la Terre, à peu près constante en valeur au cours du temps car l'orbite de la Terre est quasi circulaire. L'amplitude du mouvement d'aberration est donc environ de v/c{displaystyle v/c}, exprimé sous forme d'un angle, soit 20.49552". C'est ce que l'on appelle la constante d'aberration.

Calcul relativiste |

Le calcul précédent est valide dans le cas où v{displaystyle v} représente une vitesse faible devant celle de la lumière. C'est le phénomène d'aberration classique, similaire à la variation de la direction apparente du vent en fonction de la vitesse et la direction d'un voilier soumis à un vent constant. Pour la lumière, le calcul précédent n'est pas tout à fait exact, puisque le vecteur calculé (−ccos⁡θ−v−csin⁡θ){displaystyle {begin{pmatrix}-ccos theta -v\-csin theta end{pmatrix}}} aurait un module (ou norme) supérieur à c, ce qui est exclu par la théorie, car cela signifierait que la vitesse de la lumière serait supérieure à c dans le référentiel R′{displaystyle R'}. Il faut donc utiliser les formules de transformation relativiste des vitesses. Dans le référentiel R′{displaystyle R'}, la propagation de la lumière se fait en fait selon la direction 11+vccos⁡θ(−ccos⁡θ−v−csin⁡θ1−v2c2){displaystyle {1 over 1+{v over c}cos theta }{begin{pmatrix}-ccos theta -v\-csin theta {sqrt {1-{v^{2} over c^{2}}}}end{pmatrix}}}, de sorte que

tan⁡θ′=sin⁡θcos⁡θ+v/c1−v2c2{displaystyle tan theta '={sin theta over cos theta +v/c}{sqrt {1-{v^{2} over c^{2}}}}}

Cette formule traduit une conséquence angulaire de l'effet Doppler-Fizeau. La différence avec la formule classique est imperceptible dans le cas de la Terre, mais peut donc être calculée.

Notes et références |

Annexes |

Articles connexes |

• 
  Effet Doppler-Fizeau : le changement de référentiel se traduit également par une modification de la fréquence de l'onde reçue. L'aberration de la lumière est avec l'effet Doppler-Fizeau la traduction expérimentale de la transformation du quadri-vecteur d'onde lors d'un changement de référentiel, dans le cadre de la relativité restreinte.


• Calculs relativistes


• Révolution copernicienne

Liens externes |

• 
  (fr) Aberration de la lumière Comment nous apparait le décor quand nous nous déplaçons très vite ?


• 
  (en) Seeing Relativity (un site pédagogique expliquant divers effets de relativité restreinte dont l'aberration)

• Portail de l’astronomie